
【题目】如图,△ABC中,D为AB上一点,E为BC上一点,且AC=CD=BD=BE,∠A=40°,则∠CDE的度数为( )
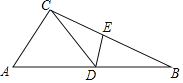
A.50°B.40°C.60°D.80°
 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】某校八年级学生小丽、小强和小红到某超市参加了社会实践活动,在活动中他们参与了某种水果的销售工作,已知该水果的进价为8元/千克,下面是他们在活动结束后的对话.
小丽:如果以10元/千克的价格销售,那么每天可售出300千克.
小强:如果以13元/千克的价格销售,那么每天可售出240千克.
小红:通过调查验证,我发现每天的销售量y(千克)与销售单价x(元)之间存在一次函数关系,每天销售200千克以上.
(1)求每天的销售量y(千克)与销售单价x(元)之间的函数关系式;
(2)该超市销售这种水果每天获取的利润达到1040元,那么销售单价为多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知![]() ,
,![]() 是一次函数
是一次函数![]() 的图象和反比例函数
的图象和反比例函数![]() 的图象的两个交点.
的图象的两个交点.
![]() 求直线
求直线![]() 与
与![]() 轴的交点
轴的交点![]() 的坐标及
的坐标及![]() 的面积;
的面积;
![]() 在
在![]() 轴上是否存在一点
轴上是否存在一点![]() ,使得
,使得![]() 的值最大?若存在,直接写出点
的值最大?若存在,直接写出点![]() 的坐标;若不存在,请说明理由;
的坐标;若不存在,请说明理由;
![]() 当点
当点![]() 在双曲线上运动时,作以
在双曲线上运动时,作以![]() 、
、![]() 为邻边的平行四边形,求平行四边形周长最小时点
为邻边的平行四边形,求平行四边形周长最小时点![]() 的坐标.
的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下面是小明同学设计的“已知底边及底边上的中线作等腰三角形”的尺规作图过程.

已知:如图 1,线段 a 和线段 b.
求作:△ABC,使得 AB = AC,BC = a,BC 边上的中线为 b.
作法:如图 ,
![]()
① 作射线 BM,并在射线 BM 上截取 BC = a;
② 作线段 BC 的垂直平分线 PQ,PQ 交 BC 于 D;
③ 以 D 为圆心,b 为半径作弧,交 PQ 于 A;
④ 连接 AB 和 AC.
则△ABC 为所求作的图形.
根据上述作图过程,回答问题:
(1)用直尺和圆规,补全图 2 中的图形;
(2)完成下面的证明:
证明:由作图可知 BC = a,AD = b.
∵ PQ 为线段 BC 的垂直平分线,点 A 在 PQ 上,
∴ AB = AC( )(填依据).
又∵线段 BC 的垂直平分线 PQ 交 BC 于 D,
∴ BD=CD.( )(填依据).
∴ AD 为 BC 边上的中线,且 AD = b.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在⊙O中,将![]() 沿弦BC所在直线折叠,折叠后的弧与直径AB相交于点D,连接CD.
沿弦BC所在直线折叠,折叠后的弧与直径AB相交于点D,连接CD.
(1)若点D恰好与点O重合,则∠ABC= °;
(2)延长CD交⊙O于点M,连接BM.猜想∠ABC与∠ABM的数量关系,并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】五一期间,小明一家一起去旅游,如图是小明设计的某旅游景点的图纸(网格是由相同的小正方形组成的,且小正方形的边长代表实际长度100m),在该图纸上可看到两个标志性景点A,B.若建立适当的平面直角坐标系,则点A(-3,1),B(-3,-3),第三个景点C(3,2)的位置已破损.
(1)请在图中标出景点C的位置;
(2)小明想从景点B开始游玩,途经景点A,最后到达景点C,求小明一家最短的行走路程(参考数据:![]() ≈6,结果保留整数).
≈6,结果保留整数).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对于一个关于![]() 的代数式
的代数式![]() ,若存在一个系数为正数关于
,若存在一个系数为正数关于![]() 的单项式
的单项式![]() ,使
,使![]() 的结果是所有系数均为整数的整式,则称单项式
的结果是所有系数均为整数的整式,则称单项式![]() 为代数式
为代数式![]() 的“整系单项式” ,例如:
的“整系单项式” ,例如:
当![]() 时,由于
时,由于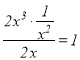 ,故
,故![]() 是
是![]() 的整系单项式;
的整系单项式;
当![]() 时,由于
时,由于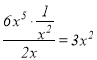 ,故
,故![]() 是
是![]() 的整系单项式;
的整系单项式;
当![]() 时,由于
时,由于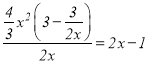 ,故
,故![]() 是
是![]() 的整系单项式;
的整系单项式;
当![]() 时,由于
时,由于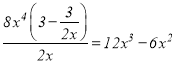 ,故
,故![]() 是
是![]() 的整系单项式;
的整系单项式;
显然,当代数式![]() 存在整系单项式
存在整系单项式![]() 时,
时,![]() 有无数个,现把次数最低,系数最小的整系单项式
有无数个,现把次数最低,系数最小的整系单项式![]() 记为
记为![]() ,例如:
,例如:![]() .
.
阅读以上材料并解决下列问题:
⑴.判断:当![]() 时,
时,![]()
![]() 的整系单项式(填“是”或“不是”);
的整系单项式(填“是”或“不是”);
⑵.当![]() 时,
时,![]() = ;
= ;
⑶.解方程: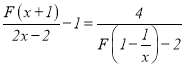 .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y1=(x-2)2+m与x轴交于点A和B,与y轴交于点C,点D是点C关于抛物线对称轴的对称点,若点A的坐标为(1,0),直线y2=kx+b经过点A,D.
(1)求抛物线的函数解析式;
(2)求点D的坐标和直线AD的函数解析式;
(3)根据图象指出,当x取何值时,y2>y1.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com