
【题目】如图,在⊙O中,将![]() 沿弦BC所在直线折叠,折叠后的弧与直径AB相交于点D,连接CD.
沿弦BC所在直线折叠,折叠后的弧与直径AB相交于点D,连接CD.
(1)若点D恰好与点O重合,则∠ABC= °;
(2)延长CD交⊙O于点M,连接BM.猜想∠ABC与∠ABM的数量关系,并说明理由.

【答案】(1) 30;(2) ∠ABM=2∠ABC,理由见解析.
【解析】
(1)根据折叠的性质和圆周角定理解答即可;
(2)作点D关于BC的对称点D',利用对称的性质和圆周角定理解答即可.
(1)∵由折叠可知:∠OBC=∠CBD,
∵点D恰好与点O重合,
∴∠COD=60°,
∴∠ABC=∠OBC=![]() ;
;
故答案为:30;
(2)∠ABM=2∠ABC,理由如下:
作点D关于BC的对称点D',连接CD',BD',
由对称可得∠DBC=∠D'BC,DC=D'C,
连接CO,D'O,AC,
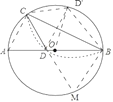
∴∠AOC=2∠ABC,∠D'OC=2∠D'BC,
∴∠AOC=∠D'OC,
∴AC=D'C,
∵DC=D'C,
∴AC=DC,
∴∠CAD=∠CDA,
∵AB是直径,
∴∠ACB=90°,
∴∠CAD+∠ABC=90°,
设∠ABC=α,则∠CAD=∠CDA=90°﹣α,
∴∠ACD=180°﹣∠CAD﹣∠CDA=2α,
即∠ACD=2∠ABC,
∵∠ABM=∠ACD,
∴∠ABM=2∠ABC.


科目:初中数学 来源: 题型:
【题目】如图,已知正方形ABCD的边长为4,以AB为一边作等边△ABE,使点E落在正方形ABCD的内部,连接AC交BE于点F,连接CE、DE,则下列说法中:①△ADE≌△BCE;②∠ACE=30°;③AF=![]() CF;④
CF;④ ![]() =2+
=2+![]() ,其中正确的有( )
,其中正确的有( )

A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
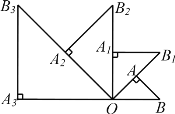
【题目】如图,△ OAB 是腰长为 1 的等腰直角三角形, OAB 90°,延长OA 至 B1 ,使 AB1 OA ,以OB1 为底,在△ OAB 外侧作等腰直角三角形OA1B1 ,再延长OA1 至 B2 , 使 A1B2 OA1 ,以OB2 为底,在△ OA1B1 外侧作等腰直角三角形OA2 B2 ,……,按此规律作等腰直角三角形OAn Bn ( n 1 , n 为正整数),回答下列问题:
(1) A3B3 的长是_____________;(2)△ OA2020 B2020 的面积是_____________.
查看答案和解析>>
科目:初中数学 来源: 题型:
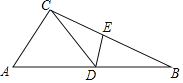
【题目】如图,△ABC中,D为AB上一点,E为BC上一点,且AC=CD=BD=BE,∠A=40°,则∠CDE的度数为( )
A.50°B.40°C.60°D.80°
查看答案和解析>>
科目:初中数学 来源: 题型:
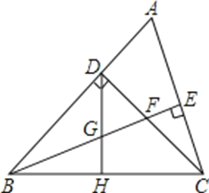
【题目】已知:如图,△ABC中,∠ABC=45°,CD⊥AB于D,BE平分∠ABC,且BE⊥AC于E,与CD相交于点F,H是BC边的中点,连结DH与BE相交于点G.
(1)求证:BF=AC;
(2)求证:CE=![]() BF.
BF.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知点![]() 在
在![]() 的
的![]() 边上,
边上,![]() 交
交![]() 于
于![]() ,
,![]() 交
交![]() 于
于![]() ,若添加条件________,则四边形
,若添加条件________,则四边形![]() 是矩形;若添加条件________,则四边形
是矩形;若添加条件________,则四边形![]() 是菱形;若添加条件________,则四边形
是菱形;若添加条件________,则四边形![]() 是正方形.
是正方形.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,将![]() 绕点
绕点![]() 顺时针旋转到
顺时针旋转到![]() 的位置,点
的位置,点![]() 、
、![]() 分别落在点
分别落在点![]() 、
、![]() 处,点
处,点![]() 在
在![]() 轴上,再将
轴上,再将![]() 绕点
绕点![]() 顺时针旋转到
顺时针旋转到![]() 的位置,点
的位置,点![]() 在
在![]() 轴上,将
轴上,将![]() 绕点
绕点![]() 顺时针旋转到
顺时针旋转到![]() 的位置,点
的位置,点![]() 在
在![]() 轴上,依次进行下去….若点
轴上,依次进行下去….若点![]() ,
,![]() ,则点
,则点![]() 的坐标为( )
的坐标为( )

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
【题目】小泽和小帅两同学分别从甲地出发,骑自行车沿同一条路到乙地参加社会实践活动.如图折线OAB和线段CD分别表示小泽和小帅离甲地的距离y(单位:千米)与时间x(单位:小时)之间函数关系的图象.根据图中提供的信息,解答下列问题:
(1)小帅的骑车速度为 千米/小时;点C的坐标为 ;
(2)求线段AB对应的函数表达式;
(3)当小帅到达乙地时,小泽距乙地还有多远?

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com