
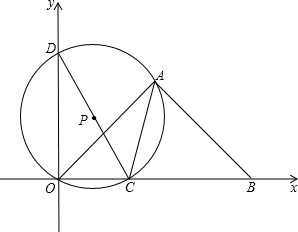
 (2013•乐清市模拟)如图,等腰Rt△ABO的斜边OB在x轴上,O是坐标原点,点A在第一象限内,BO=2,点C(t,0)是线段OB上一动点(不与O,B重合),△OAC的外接圆⊙P与y轴的另一交点为D.
(2013•乐清市模拟)如图,等腰Rt△ABO的斜边OB在x轴上,O是坐标原点,点A在第一象限内,BO=2,点C(t,0)是线段OB上一动点(不与O,B重合),△OAC的外接圆⊙P与y轴的另一交点为D.| OC2+OD2 |
| t2+(2-t)2 |
| 2 |
| 2-t |
| 2-t |
| t |
| 2 |
| t |
| (AE+AF)2-AE2-AF2 |
| 2 |
| 1 |
| 2 |
| 2t2-4t+4 |
| -t2+2t |
| 2(t2-2t)+4 |
| -(t2-2t) |
| 4 |
| -(t-1)2+1 |
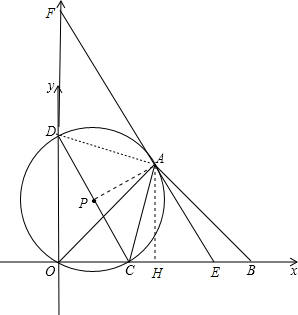 (1)证明:连结AD,如图,
(1)证明:连结AD,如图,
|
| OC2+OD2 |
| t2+(2-t)2 |
| 2(t-1)2+2 |
| 2 |
| 2 |
| 2-t |
| 2 |
| 2-t |
| 2-t |
| t |
| 2-t |
| t |
| 2 |
| 2-t |
| 2 |
| t |
| (AE+AF)2-AE2-AF2 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 2 |
| 2-t |
| 2 |
| t |
| 2t2-4t+4 |
| -t2+2t |
| 2(t2-2t)+4 |
| -(t2-2t) |
| 4 |
| -(t-1)2+1 |


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
 (2013•乐清市模拟)某校开展大课间活动,某班同学积极响应,某班同学参加大课间活动项目情况的扇形统计图该班同学参加体育项目情况的扇形统计图如图所示,由图可知参加人数最多的活动是( )
(2013•乐清市模拟)某校开展大课间活动,某班同学积极响应,某班同学参加大课间活动项目情况的扇形统计图该班同学参加体育项目情况的扇形统计图如图所示,由图可知参加人数最多的活动是( )查看答案和解析>>
科目:初中数学 来源: 题型:
 (2013•乐清市模拟)如图,点D在△ABC的边BC上,过点D作DF∥AB,交AC于点E,连结BF,已知BD:DC=1:2,DE:EF=1:3,则S△ABC:S△BDF=( )
(2013•乐清市模拟)如图,点D在△ABC的边BC上,过点D作DF∥AB,交AC于点E,连结BF,已知BD:DC=1:2,DE:EF=1:3,则S△ABC:S△BDF=( )查看答案和解析>>
科目:初中数学 来源: 题型:
 (2013•乐清市模拟)如图,在四边形ABCD中,AD∥BC,AD⊥AB,AB=BC=5,AD=1,E是AB所在直线上的一个动点,当
(2013•乐清市模拟)如图,在四边形ABCD中,AD∥BC,AD⊥AB,AB=BC=5,AD=1,E是AB所在直线上的一个动点,当| 4 |
| 5 |
5+
| ||
| 2 |
5-
| ||
| 2 |
| 4 |
| 5 |
5+
| ||
| 2 |
5-
| ||
| 2 |
查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
 (2013•乐清市模拟)如图,在△ABC中,点O在AB边上,以O为圆心的圆经过A,C两点,交AB于点D,且2∠A+∠B=90°,
(2013•乐清市模拟)如图,在△ABC中,点O在AB边上,以O为圆心的圆经过A,C两点,交AB于点D,且2∠A+∠B=90°,查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com