Question

5．如图1，已知矩形纸片ABCD中，AB=6cm，若将该纸片沿着过点B的直线折叠（折痕为BM），点A恰好落在CD边的中点P处．

（1）求矩形ABCD的边AD的长．
（2）若P为CD边上的一个动点，折叠纸片，使得A与P重合，折痕为MN，其中M在边AD上，N在边BC上，如图2所示．设DP=x cm，DM=y cm，试求y与x的函数关系式，并指出自变量x的取值范围．
（3）①当折痕MN的端点N在AB上时，求当△PCN为等腰三角形时x的值；
②当折痕MN的端点M在CD上时，设折叠后重叠部分的面积为S，试求S与x之间的函数关系式．

Answer 1

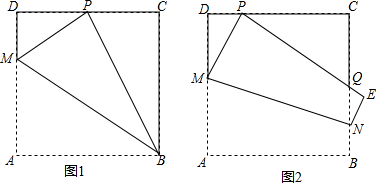
分析 （1）由折叠的性质得出BP=AB=6cm，由矩形的性质得出∠C=90°，CD=AB=6cm，得出PC，根据勾股定理求出BC即可；
（2）由折叠的性质得出AM=MP=3$\sqrt{3}$-y，再根据勾股定理得出x²+y²=（3$\sqrt{3}$-y）²，即可求出y与x的函数关系式和x的取值范围；
（3）①根据题意得出只可能NC=NP；过N点作NQ⊥CD于Q，得出PQ=CQ，根据勾股定理得出方程，解方程即可；
 ②当点M在CD上时，N在AB上；先证出四边形ANPM是菱形，设MP=y，根据勾股定理得出：（x-y）²+（3$\sqrt{3}$）²=y²．求出y，即可得出S与x的函数关系式．

解答 解：（1）根据题意得：BP=AB=6cm，
∵四边形ABCD是矩形，
∴∠C=90°，AB∥CD，CD=AB=6cm，
∵P为CD的中点，
∴PC=$\frac{1}{2}$CD=3cm，
根据勾股定理得：BC=$\sqrt{B{P}^{2}-P{C}^{2}}$=$\sqrt{{6}^{2}-{3}^{2}}$=3$\sqrt{3}$，
∴AD=3$\sqrt{3}$（cm）；     
（2）根据题意得：AM=MP=3$\sqrt{3}$-y，在Rt△MPD中，PD²+MD²=MP²，
∴x²+y²=（3$\sqrt{3}$-y）²．
∴y=-$\frac{\sqrt{3}}{18}$x²+$\frac{3\sqrt{3}}{2}$，
其中，0＜x＜3；
（3）①当点N在AB上，x≥3，
∴PC≤3，而PN≥3$\sqrt{3}$，NC≥3$\sqrt{3}$．
∴△PCN为等腰三角形，只可能NC=NP；
过N点作NQ⊥CD于Q，如图3所示：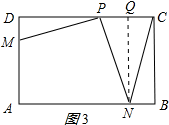
则PQ=CQ=$\frac{1}{2}$（6-x）=3-$\frac{1}{2}$x，NP=AN=6-CQ=3+$\frac{1}{2}$x，
在Rt△NPQ中，PQ²+NQ²=NP²．
∴（3-$\frac{1}{2}$x）²+（3$\sqrt{3}$）²=（3+$\frac{1}{2}$x）²．
解得：x=$\frac{9}{2}$．
②当点M在CD上时，N在AB上；如图4所示：
根据题意得：MN垂直平分AP，
∴OA=OP，
∵AB∥CD，OM=ON，
∴四边形ANPM是平行四边形，
又∵PM=AM，
∴四边形ANPM是菱形，
∴折叠后重叠部分的面积S=△PMN的面积，
设MP=y，在Rt△ADM中，AD²+DM²=AM²，
∴（x-y）²+（3$\sqrt{3}$）²=y²．
解得：y=$\frac{{x}^{2}+27}{2x}$，
∴S=$\frac{1}{2}$MP•BC=$\frac{1}{2}$y•3$\sqrt{3}$=$\frac{3\sqrt{3}{x}^{2}+81\sqrt{3}}{4x}$．

点评 本题是四边形综合题目，考查了矩形的性质、勾股定理、等腰三角形的性质、菱形的判定、垂直平分线的性质、三角形面积的计算等知识；本题难度较大，综合性强，特别是（3）中，需要通过作辅助线运用勾股定理和证明四边形是菱形才能得出结果．