
【题目】已知二次函数 ![]() 的图象与x轴交于A,B两点(点A在点B的左边),与y轴交于点C,顶点为D.
的图象与x轴交于A,B两点(点A在点B的左边),与y轴交于点C,顶点为D.
(1)求以A,B,C,D为顶点的四边形的面积;
(2)在抛物线上是否存在点P,使得△ABP的面积是△ABC的面积的2倍?若存在,求出点P的坐标;若不存在,请说明理由。
【答案】
(1)解:令y=0, x26x+5=0 ,
∴ x1=1,x2=5,
∴A(1,0),B(5,0),
令x=0,
∴y=5,
∴C(0,5)
∵ y=x26x+5=(x3)24 ,
∴D(3,-4)
∴S四边形ACBD=S△ABD+S△ABC=![]() +
+![]() =18 .
=18 .
(2)解:∵ S△ABP=2S△ABC,且两个三角形底边相同,
∴ |yP|=2|yC|=10 ,
又∵ ymin=4 ,
∴ yP=10 ,
∴ P1(3+![]() ,10),P2(3-
,10),P2(3-![]() ,10).
,10).
【解析】(1)根据题意令y=0得出A(1,0),B(5,0),令x=0得C(0,5),将抛物线解析式化成顶点式得 D(3,-4),从而求出
∴S四边形ACBD=S△ABD+S△ABC=![]() +
+![]() =18 .
=18 .
(2)根据 S△ABP=2S△ABC,且底边相同,得出|yP|=2|yC|=10 ,再由已知条件得yP=10 , 从而得P点坐标为 P1(3+![]() ,10),P2(3-
,10),P2(3-![]() ,10).
,10).
【考点精析】认真审题,首先需要了解抛物线与坐标轴的交点(一元二次方程的解是其对应的二次函数的图像与x轴的交点坐标.因此一元二次方程中的b2-4ac,在二次函数中表示图像与x轴是否有交点.当b2-4ac>0时,图像与x轴有两个交点;当b2-4ac=0时,图像与x轴有一个交点;当b2-4ac<0时,图像与x轴没有交点.),还要掌握三角形的面积(三角形的面积=1/2×底×高)的相关知识才是答题的关键.


 名题金卷系列答案
名题金卷系列答案科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,直线l1的解析式为y=-x,直线l2与l1交于点A(a,-a),与y轴交于点B(0,b),其中a,b满足(a+3)2+![]() =0.
=0.
(1)求直线l2的解析式;
(2)在平面直角坐标系中第二象限有一点P(m,5),使得S△AOP=S△AOB,请求出点P的坐标;
(3)已知平行于y轴左侧有一动直线,分别与l1,l2交于点M、N,且点M在点N的下方,点Q为y轴上一动点,且△MNQ为等腰直角三角形,请求出满足条件的点Q的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,一次函数y=﹣![]() x+b的图象与y轴交于点B(0,2),与反比例函数y=
x+b的图象与y轴交于点B(0,2),与反比例函数y=![]() 的图象交于点A(4,﹣1).
的图象交于点A(4,﹣1).
(1)求反比例函数的表达式和一次函数表达式;
(2)如果点P是x轴上的一点,且△ABP的面积是3,求P点的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在锐角三角形ABC中,直线l为BC的中垂线,射线m为∠ABC的角平分线,直线l与m相交于点P.若∠BAC=60°,∠ACP=24°,则∠ABP的度数是( )

A. 24° B. 30° C. 32° D. 36°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明同学在做作业时,遇到这样一道几何题:
已知:如图1,l1∥l2∥l3,点A、M、B分别在直线l1,l2,l3上,MC平分∠AMB,∠1=28°,∠2=70°.求:∠CMD的度数.
小明想了许久没有思路,就去请教好朋友小坚,小坚给了他如图2所示的提示:
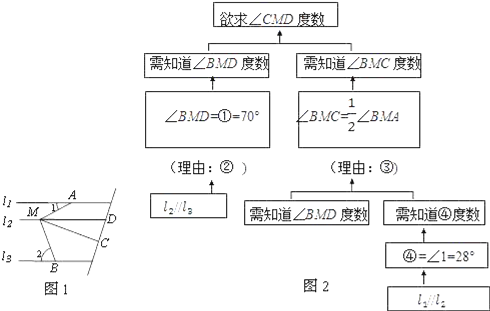
请问小坚的提示中①是∠ ,④是∠ .
理由②是: ;
理由③是: ;
∠CMD的度数是 °.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中,∠BAC=90°,点D是BC上一点,将△ABD沿AD翻折后得到△AED,边AE交BC于点F.


(1)如图①,当AE⊥BC时,写出图中所有与∠B相等的角: ;所有与∠C相等的角: .
(2)若∠C-∠B=50°,∠BAD=x°(0<x≤45) .
① 求∠B的度数;
②是否存在这样的x的值,使得△DEF中有两个角相等.若存在,并求x的值;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在边长为4的正方形ABCD中,对角线AC,BD相交于点O,点E是AD边上一点,连接CE,把△CDE沿CE翻折,得到△CPE,EP交AC于点F,CP交BD于点G,连接PO,若PO∥BC,则四边形OFPG的面积是 . 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将放在每个小正方形的边长为1的网格中,点A,B,C均落在格点上.
(1)计算AB边的长等于;
(2)在如图所示的网格中,用无刻度的直尺,画出一个以AB为一边的矩形,使矩形的面积等于△ABC的面积,并简要说明画图的方法(不要求证明).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com