
【题目】如图,在平面直角坐标系xOy中,直线y=﹣ ![]() x+1与x轴、y轴分别相交于点A、B,将△AOB沿直线AB翻折,点O落在点O′处,则点O′的坐标为 .
x+1与x轴、y轴分别相交于点A、B,将△AOB沿直线AB翻折,点O落在点O′处,则点O′的坐标为 . 
【答案】( ![]() ,
, ![]() )
)
【解析】解:在y=﹣ ![]() x+1中,令x=0,得y=1,令y=0,得x=2,
x+1中,令x=0,得y=1,令y=0,得x=2,
∴A(2,0),B(0,1),
∴OA=2,OB=1,
∵将△AOB沿直线AB翻折,点O落在点O′处,
∴AO′=AO=2,BO′=BO=1,∠AO′B=90°,
延长AC交y轴于C,
过O′作O′D⊥OA于D,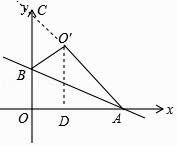
∴∠CO′B=∠AOC=90°,
∵∠BCO′=∠ACO,
∴△BCO′∽△ACO,
∴ ![]() ,
,
∴ ![]() =
= ![]() =
= ![]() ,
,
∴BC= ![]() ,CO′=
,CO′= ![]() ,
,
∴OC= ![]() ,AC=
,AC= ![]() ,
,
∵O′D⊥OA,
∴O′D∥OC,
∴△ADO′∽△AOC,
∴ ![]() =
= ![]() =
= ![]() ,即
,即 ![]() =
= ![]() =
= ![]() ,
,
∴DO′= ![]() ,AD=
,AD= ![]() ,
,
∴OD= ![]() ,
,
∴O′( ![]() ,
, ![]() ),
),
所以答案是:( ![]() ,
, ![]() ).
).
【考点精析】解答此题的关键在于理解翻折变换(折叠问题)的相关知识,掌握折叠是一种对称变换,它属于轴对称,对称轴是对应点的连线的垂直平分线,折叠前后图形的形状和大小不变,位置变化,对应边和角相等,以及对相似三角形的性质的理解,了解对应角相等,对应边成比例的两个三角形叫做相似三角形.


 黎明文化寒假作业系列答案
黎明文化寒假作业系列答案科目:初中数学 来源: 题型:
【题目】如图,函数y= ![]() 和y=﹣
和y=﹣ ![]() 的图象分别是l1和l2 . 设点P在l1上,PC⊥x轴,垂足为C,交l2于点A,PD⊥y轴,垂足为D,交l2于点B,则△PAB的面积为 .
的图象分别是l1和l2 . 设点P在l1上,PC⊥x轴,垂足为C,交l2于点A,PD⊥y轴,垂足为D,交l2于点B,则△PAB的面积为 . 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知△ABC中,AB=AC,O为BC的中点,AB与⊙O相切于点D. 
(1)求证:AC是⊙O的切线;
(2)若∠B=33°,⊙O的半径为1,求BD的长.(结果精确到0.01)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】神仙居景区门票价格80元/人,景区为吸引游客,对门票价格进行动态管理,非节假日打a折,节假日期间,10人以下(包 括10人)不打折,10人以上超过10人的部分打b折,设游客为x人,门票费用为y元,非节假日门票费用y1(元)及节假日门票费用y2(元)与游客x(人)之间的函数关系如图所示.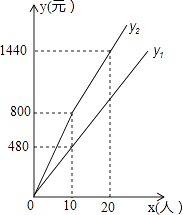
(1)a= , b=;
(2)直接写出y1、y2与x之间的函数关系式;
(3)导游小王6月10日(非节假日)带A旅游团,6月20日(端午节)带B旅游团到神仙居景区旅游,两团共计50人,两次共付门票费用3040元,求A、B两个旅游团各多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在坡角为30°的山坡上有一铁塔AB,其正前方矗立着一大型广告牌,当阳光与水平线成45°角时,测得铁塔AB落在斜坡上 的影子BD的长为6米,落在广告牌上的影子CD的长为4米,求铁塔AB的高(AB,CD均与水平面垂直,结果保留根号).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,点A、B的坐标分别为(0,3)、(7,0),点C在第一象限,AC∥x轴,∠OBC=45°.
(1)求点C的坐标;
(2)点D在线段AC上,CD=1,点E的坐标为(n,0),在直线DE的右侧作∠DEG=45°,直线EG与直线BC相交于点F,设BF=m,当n<7且n≠0时,求m关于n的函数解析式,并直接写出n的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,某中学在教学楼前新建了一座雕塑AB,为了测量雕塑的高度,小明在二楼找到一点C,利用三角尺测得雕塑顶端点A的仰角∠QCA为45°,底部点B的俯角∠QCB为30°,小华在五楼找到一点D,利用三角尺测得点A的俯角∠PDA为60°,若AD为8m,则雕塑AB的高度为多少?(结果精确到0.1m,参考数据: ![]() ≈1.73).
≈1.73).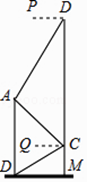
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知点C(1,0),直线y=﹣x+7与两坐标轴分别交于A、B两点,D、E分别是AB,OA上的动点,当△CDE周长最小时,点D坐标为 . 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,如图,AB是⊙O的直径,点C为⊙O上一点,OF⊥BC于点F,交⊙O于点E,AE与BC交于点H,点D为OE的延长线上一点,且∠ODB=∠AEC.
(1)求证:BD是⊙O的切线;
(2)求证:CE2=EHEA;
(3)若⊙O的半径为5,sinA=![]() ,求BH的长。
,求BH的长。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com