
【题目】等边△ABC中,点E在AB上,点D在CA的延长线上,且ED=EC.试探索以下问题: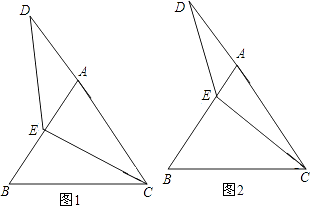
(1)如图1,当E为AB中点时,试确定线段AD与BE的大小关系,请你直接写出结论:
(2)如图2,若点E为线段AB上任意一点,(1)中结论是否成立,若成立,请证明结论,若不成立,请说明理由。
【答案】
(1)解:AD=BE
(2)解:过点E作EF∥AC交BC于点F,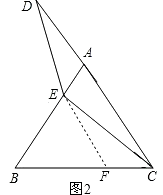
∴∠EFB=∠ACB,∠BEF=∠BAC,∠FEC=∠ECA,
∵△ABC是等边三角形,
∴∠ACB=∠BAC=∠B=60°,
∴∠EFB=∠BEF=∠B=60°,
∴△BEF是等边三角形,
∴BE=EF,
∵ED=EC,
∴∠D=∠ECA,
∴∠D=∠FEC,
∵∠BFE=∠BAC=60°,
∴∠EAD=∠CFE=120°,
在△AED和△FCE中,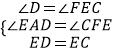
∴△AED≌△FCE(AAS),
∴AD=FE,
∴AD=BE
【解析】根据平行线的性质和等边三角形的性质、判定,得到△BEF是等边三角形,由角的和差和等边三角形的性质,得到角、边相等,根据全等三角形的判定方法AAS,得到△AED≌△FCE,得到全等三角形的对应边相等.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图1,在正方形ABCD的外侧,作两个等边三角形ADE和DCF,连接AF,BE.
(1)请判断:AF与BE的数量关系是 ,位置关系是 ;
(2)如图2,若将条件“两个等边三角形ADE和DCF”变为“两个等腰三角形ADE和DCF,且EA=ED=FD=FC”,第(1)问中的结论是否仍然成立?请作出判断并给予说明;
(3)若三角形ADE和DCF为一般三角形,且AE=DF,ED=FC,第(1)问中的结论都能成立吗?请直接写出你的判断.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】关于体育选考项目统计图
项目 | 频数 | 频率 |
A | 80 | b |
B | c | 0.3 |
C | 20 | 0.1 |
D | 40 | 0.2 |
合计 | a | 1 |
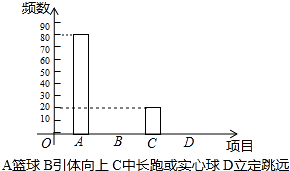
(1)求出表中a,b,c的值,并将条形统计图补充完整. 表中a= , b= , c= .
(2)如果有3万人参加体育选考,会有多少人选择篮球?
查看答案和解析>>
科目:初中数学 来源: 题型:
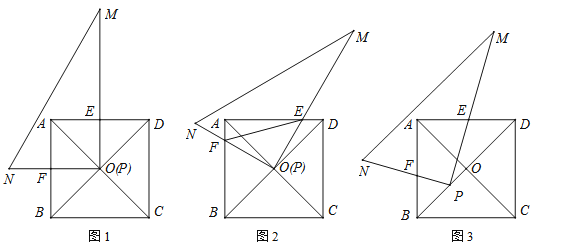
【题目】在正方形ABCD中,对角线AC与BD交于点O;在Rt△PMN中,∠MPN=90°.
(1)如图1,若点P与点O重合且PM⊥AD、PN⊥AB,分别交AD、AB于点E、F,请直接写出PE与PF的数量关系;
(2)将图1中的Rt△PMN绕点O顺时针旋转角度α(0°<α<45°).
①如图2,在旋转过程中(1)中的结论依然成立吗?若成立,请证明;若不成立,请说明理由;
②如图2,在旋转过程中,当∠DOM=15°时,连接EF,若正方形的边长为2,请直接写出线段EF的长;
③如图3,旋转后,若Rt△PMN的顶点P在线段OB上移动(不与点O、B重合),当BD=3BP时,猜想此时PE与PF的数量关系,并给出证明;当BD=mBP时,请直接写出PE与PF的数量关系.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下面材料:
小明遇到这样一个问题:如图1,△ABC中,AB=AC,点D在BC边上,∠DAB=∠ABD,BE⊥AD,垂足为E,求证:BC=2AE.
小明经探究发现,过点A作AF⊥BC,垂足为F,得到∠AFB=∠BEA,从而可证△ABF≌△BAE(如图2),使问题得到解决.
(1)根据阅读材料回答:△ABF与△BAE全等的条件是 AAS(填“SSS”、“SAS”、“ASA”、“AAS”或“HL”中的一个)
参考小明思考问题的方法,解答下列问题:
(2)如图3,△ABC中,AB=AC,∠BAC=90°,D为BC的中点,E为DC的中点,点F在AC的延长线上,且∠CDF=∠EAC,若CF=2,求AB的长;
(3)如图4,△ABC中,AB=AC,∠BAC=120°,点D、E分别在AB、AC边上,且AD=kDB(其中0<k<![]() ),∠AED=∠BCD,求
),∠AED=∠BCD,求![]() 的值(用含k的式子表示).
的值(用含k的式子表示).

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com