
【题目】不属于中心对称图形的是( )
A.长方形B.平行四边形
C.等腰直角三角形D.线段
 小学学习好帮手系列答案
小学学习好帮手系列答案 小学同步三练核心密卷系列答案
小学同步三练核心密卷系列答案科目:初中数学 来源: 题型:
【题目】下列说法中正确的是( )
A.掷两枚质地均匀的硬币,“两枚硬币都是正面朝上”这一事件发生的概率为 ![]()
B.“对角线相等且相互垂直平分的四边形是正方形”这一事件是必然事件
C.“同位角相等”这一事件是不可能事件
D.“钝角三角形三条高所在直线的交点在三角形外部”这一事件是随机事件
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】等腰△ABC的底边BC=8cm,腰长AB=5cm,一动点P在底边上从点B开始向点C以0.25cm/秒的速度运动,当点P运动到PA与腰垂直的位置时,点P运动的时间应为_____秒.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某企业为了解员工给灾区“爱心捐款”的情况,随机抽取部分员工的捐款金额整理绘制成如图所示的直方图,根据图中信息,下列结论错误的是( )
A.样本中位数是200元
B.样本容量是20
C.该企业员工捐款金额的平均数是180元
D.该企业员工最大捐款金额是500元
查看答案和解析>>
科目:初中数学 来源: 题型:
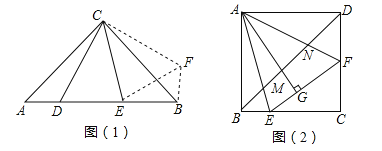
【题目】问题:如图(1),在Rt△ACB中,∠ACB=90°,AC=CB,∠DCE=45°,试探究AD、DE、EB满足的等量关系.
[探究发现]
小聪同学利用图形变换,将△CAD绕点C逆时针旋转90°得到△CBH,连接EH,由已知条件易得∠EBH=90°,∠ECH=∠ECB+∠BCH=∠ECB+∠ACD=45°.根据“边角边”,可证△CEH≌ ,得EH=ED.
在Rt△HBE中,由 定理,可得BH2+EB2=EH2,由BH=AD,可得AD、DE、EB之间的等量关系是 .
[实践运用]
(1)如图(2),在正方形ABCD中,△AEF的顶点E、F分别在BC、CD边上,高AG与正方形的边长相等,求∠EAF的度数;
(2)在(1)条件下,连接BD,分别交AE、AF于点M、N,若BE=2,DF=3,BM=2![]() ,运用小聪同学探究的结论,求正方形的边长及MN的长.
,运用小聪同学探究的结论,求正方形的边长及MN的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中,AB=AC,点F是BC延长线上一点,以CF为边,作菱形CDEF,使菱形CDEF与点A在BC的同侧,连接BE,点G是BE的中点,连接AG、DG.
(1)如图①,当∠BAC=∠DCF=90°时,直接写出AG与DG的位置和数量关系;
(2)如图②,当∠BAC=∠DCF=60°时,试探究AG与DG的位置和数量关系,
(3)当∠BAC=∠DCF=α时,直接写出AG与DG的数量关系.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲乙两地相距200km , 快车速度为120 ![]() ,慢车速度为80
,慢车速度为80 ![]() ,慢车从甲地出发,快车从乙地出发,
,慢车从甲地出发,快车从乙地出发,
(1)如果两车同时出发,相向而行,出发后几时两车相遇?相遇时离甲地多远?
(2)如果两车同时出发,同向(从乙开始向甲方向)而行,出发后几时两车相遇?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】等边△ABC中,点E在AB上,点D在CA的延长线上,且ED=EC.试探索以下问题: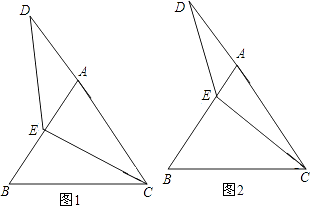
(1)如图1,当E为AB中点时,试确定线段AD与BE的大小关系,请你直接写出结论:
(2)如图2,若点E为线段AB上任意一点,(1)中结论是否成立,若成立,请证明结论,若不成立,请说明理由。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com