
ЁОЬтФПЁПдкЁїABCжаЃЌAB=ACЃЌЕуFЪЧBCбгГЄЯпЩЯвЛЕуЃЌвдCFЮЊБпЃЌзїСтаЮCDEFЃЌЪЙСтаЮCDEFгыЕуAдкBCЕФЭЌВрЃЌСЌНгBEЃЌЕуGЪЧBEЕФжаЕуЃЌСЌНгAGЁЂDGЃЎ
ЃЈ1ЃЉШчЭМЂйЃЌЕБЁЯBAC=ЁЯDCF=90ЁуЪБЃЌжБНгаДГіAGгыDGЕФЮЛжУКЭЪ§СПЙиЯЕЃЛ
ЃЈ2ЃЉШчЭМЂкЃЌЕБЁЯBAC=ЁЯDCF=60ЁуЪБЃЌЪдЬНОПAGгыDGЕФЮЛжУКЭЪ§СПЙиЯЕЃЌ
ЃЈ3ЃЉЕБЁЯBAC=ЁЯDCF=ІСЪБЃЌжБНгаДГіAGгыDGЕФЪ§СПЙиЯЕЃЎ

ЁОД№АИЁПЃЈ1ЃЉAGЁЭDGЃЌAG=DGЃЛЃЈ2ЃЉAGЁЭGDЃЌAG=![]() DGЃЛЃЈ3ЃЉDG=AGtan
DGЃЛЃЈ3ЃЉDG=AGtan![]() ЃЎ
ЃЎ
ЁОНтЮіЁП
ЪдЬтЗжЮіЃКЃЈ1ЃЉбгГЄDGгыBCНЛгкHЃЌСЌНгAHЁЂADЃЌЯШжЄЁїBGHЁеЁїEGDЧѓЕУBH=EDЃЌHG=DGЃЌЕУГіBH=DCЃЌдйжЄЁїABHЁеЁїACDЃЌЕУГіЁЯBAH=ЁЯCADЃЌAH=ADЃЌНјЖјЧѓЕУЁЯHAD=90ЁуЃЌМДПЩЧѓЕУAGЁЭGDЃЌAG=GDЃЛ
ЃЈ2ЃЉбгГЄDGгыBCНЛгкHЃЌСЌНгAHЁЂADЃЌЯШжЄЁїBGHЁеЁїEGDЧѓЕУBH=EDЃЌHG=DGЃЌЕУГіBH=DCЃЌдйжЄЁїABHЁеЁїACDЃЌЕУГіЁЯBAH=ЁЯCADЃЌAH=ADЃЌНјЖјЧѓЕУЁїHADЪЧЕШБпШ§НЧаЮЃЌМДПЩжЄЕУAGЁЭGDЃЌAG=![]() DGЃЛ
DGЃЛ
ЃЈ3ЃЉбгГЄDGгыBCНЛгкHЃЌСЌНгAHЁЂADЃЌЯШжЄЁїBGHЁеЁїEGDЧѓЕУBH=EDЃЌHG=DGЃЌЕУГіBH=DCЃЌдйжЄЁїABHЁеЁїACDЃЌЕУГіЁЯBAH=ЁЯCADЃЌAH=ADЃЌНјЖјЧѓЕУЁїHADЪЧЕШбќШ§НЧаЮЃЌМДПЩжЄЕУDG=AGtan![]() ЃЎ
ЃЎ
ЪдЬтНтЮіЃКЃЈ1ЃЉAGЁЭDGЃЌAG=DGЃЌжЄУїШчЯТЃКбгГЄDGгыBCНЛгкHЃЌСЌНгAHЁЂADЃЌЁпЫФБпаЮDCEFЪЧе§ЗНаЮЃЌЁрDE=DCЃЌDEЁЮCFЃЌЁрЁЯGBH=ЁЯGEDЃЌЁЯGHB=ЁЯGDEЃЌЁпGЪЧBCЕФжаЕуЃЌЁрBG=EGЃЌдкЁїBGHКЭЁїEGDжаЃЌЁпЁЯGBH=ЁЯGEDЃЌЁЯGHB=ЁЯGDEЃЌBG=EGЃЌЁрЁїBGHЁеЁїEGDЃЈAASЃЉЃЌЁрBH=EDЃЌHG=DGЃЌЁрBH=DCЃЌЁпAB=ACЃЌЁЯBAC=90ЁуЃЌЁрЁЯABC=ЁЯACB=45ЁуЃЌЁпЁЯDCF=90ЁуЃЌЁрЁЯDCB=90ЁуЃЌЁрЁЯACD=45ЁуЃЌЁрЁЯABH=ЁЯACD=45ЁуЃЌдкЁїABHКЭЁїACDжаЃЌЁпAB=ACЃЌЁЯABH=ЁЯACDЃЌBH=CDЃЌЁрЁїABHЁеЁїACDЃЈSASЃЉЃЌЁрЁЯBAH=ЁЯCADЃЌAH=ADЃЌЁпЁЯBAH+ЁЯHAC=90ЁуЃЌЁрЁЯCAD+ЁЯHAC=90ЁуЃЌМДЁЯHAD=90ЁуЃЌЁрAGЁЭGDЃЌAG=GDЃЛ
ЃЈ2ЃЉAGЁЭGDЃЌAG=![]() DGЃЛжЄУїШчЯТЃКбгГЄDGгыBCНЛгкHЃЌСЌНгAHЁЂADЃЌЁпЫФБпаЮDCEFЪЧе§ЗНаЮЃЌЁрDE=DCЃЌDEЁЮCFЃЌЁрЁЯGBH=ЁЯGEDЃЌЁЯGHB=ЁЯGDEЃЌЁпGЪЧBCЕФжаЕуЃЌЁрBG=EGЃЌдкЁїBGHКЭЁїEGDжаЃЌЁпЁЯGBH=ЁЯGEDЃЌЁЯGHB=ЁЯGDEЃЌBG=EGЃЌЁрЁїBGHЁеЁїEGDЃЈAASЃЉЃЌЁрBH=EDЃЌHG=DGЃЌЁрBH=DCЃЌЁпAB=ACЃЌЁЯBAC=ЁЯDCF=60ЃЌЁрЁЯABC=60ЁуЃЌЁЯACD=60ЁуЃЌЁрЁЯABC=ЁЯACD=60ЁуЃЌдкЁїABHКЭЁїACDжаЃЌЁпAB=ACЃЌЁЯABH=ЁЯACDЃЌBH=CDЃЌЁрЁїABHЁеЁїACDЃЈSASЃЉЃЌЁрЁЯBAH=ЁЯCADЃЌAH=ADЃЌЁрЁЯBAC=ЁЯHAD=60ЁуЃЌЁрAGЁЭHDЃЌЁЯHAG=ЁЯDAG=30ЁуЃЌЁрtanЁЯDAG=tan30Ёу=
DGЃЛжЄУїШчЯТЃКбгГЄDGгыBCНЛгкHЃЌСЌНгAHЁЂADЃЌЁпЫФБпаЮDCEFЪЧе§ЗНаЮЃЌЁрDE=DCЃЌDEЁЮCFЃЌЁрЁЯGBH=ЁЯGEDЃЌЁЯGHB=ЁЯGDEЃЌЁпGЪЧBCЕФжаЕуЃЌЁрBG=EGЃЌдкЁїBGHКЭЁїEGDжаЃЌЁпЁЯGBH=ЁЯGEDЃЌЁЯGHB=ЁЯGDEЃЌBG=EGЃЌЁрЁїBGHЁеЁїEGDЃЈAASЃЉЃЌЁрBH=EDЃЌHG=DGЃЌЁрBH=DCЃЌЁпAB=ACЃЌЁЯBAC=ЁЯDCF=60ЃЌЁрЁЯABC=60ЁуЃЌЁЯACD=60ЁуЃЌЁрЁЯABC=ЁЯACD=60ЁуЃЌдкЁїABHКЭЁїACDжаЃЌЁпAB=ACЃЌЁЯABH=ЁЯACDЃЌBH=CDЃЌЁрЁїABHЁеЁїACDЃЈSASЃЉЃЌЁрЁЯBAH=ЁЯCADЃЌAH=ADЃЌЁрЁЯBAC=ЁЯHAD=60ЁуЃЌЁрAGЁЭHDЃЌЁЯHAG=ЁЯDAG=30ЁуЃЌЁрtanЁЯDAG=tan30Ёу=![]() ЃЌЁрAG=
ЃЌЁрAG=![]() DGЃЛ
DGЃЛ
ЃЈ3ЃЉDG=AGtan![]() ЃЛжЄУїШчЯТЃКбгГЄDGгыBCНЛгкHЃЌСЌНгAHЁЂADЃЌЁпЫФБпаЮDCEFЪЧе§ЗНаЮЃЌЁрDE=DCЃЌDEЁЮCFЃЌЁрЁЯGBH=ЁЯGEDЃЌЁЯGHB=ЁЯGDEЃЌЁпGЪЧBCЕФжаЕуЃЌЁрBG=EGЃЌдкЁїBGHКЭЁїEGDжаЃЌЁЯGBH=ЁЯGEDЃЌЁЯGHB=ЁЯGDEЃЌBG=EGЃЌЁрЁїBGHЁеЁїEGDЃЈAASЃЉЃЌЁрBH=EDЃЌHG=DGЃЌЁрBH=DCЃЌЁпAB=ACЃЌЁЯBAC=ЁЯDCF=ІСЃЌЁрЁЯABC=90ЁуЉ
ЃЛжЄУїШчЯТЃКбгГЄDGгыBCНЛгкHЃЌСЌНгAHЁЂADЃЌЁпЫФБпаЮDCEFЪЧе§ЗНаЮЃЌЁрDE=DCЃЌDEЁЮCFЃЌЁрЁЯGBH=ЁЯGEDЃЌЁЯGHB=ЁЯGDEЃЌЁпGЪЧBCЕФжаЕуЃЌЁрBG=EGЃЌдкЁїBGHКЭЁїEGDжаЃЌЁЯGBH=ЁЯGEDЃЌЁЯGHB=ЁЯGDEЃЌBG=EGЃЌЁрЁїBGHЁеЁїEGDЃЈAASЃЉЃЌЁрBH=EDЃЌHG=DGЃЌЁрBH=DCЃЌЁпAB=ACЃЌЁЯBAC=ЁЯDCF=ІСЃЌЁрЁЯABC=90ЁуЉ![]() ЃЌЁЯACD=90ЁуЉ
ЃЌЁЯACD=90ЁуЉ![]() ЃЌЁрЁЯABC=ЁЯACDЃЌдкЁїABHКЭЁїACDжаЃЌAB=ACЃЌЁЯABH=ЁЯACDЃЌBH=CDЃЌЁрЁїABHЁеЁїACDЃЈSASЃЉЃЌЁрЁЯBAH=ЁЯCADЃЌAH=ADЃЌЁрЁЯBAC=ЁЯHAD=ІСЃЛЁрAGЁЭHDЃЌЁЯHAG=ЁЯDAG=
ЃЌЁрЁЯABC=ЁЯACDЃЌдкЁїABHКЭЁїACDжаЃЌAB=ACЃЌЁЯABH=ЁЯACDЃЌBH=CDЃЌЁрЁїABHЁеЁїACDЃЈSASЃЉЃЌЁрЁЯBAH=ЁЯCADЃЌAH=ADЃЌЁрЁЯBAC=ЁЯHAD=ІСЃЛЁрAGЁЭHDЃЌЁЯHAG=ЁЯDAG=![]() ЃЌЁрtanЁЯDAG=tan
ЃЌЁрtanЁЯDAG=tan![]() =
=![]() ЃЌЁрDG=AGtan
ЃЌЁрDG=AGtan![]() ЃЎ
ЃЎ




| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
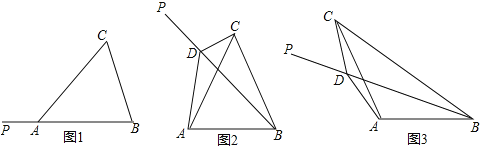
ЁОЬтФПЁПШчЭМ1ЃЌдкЁїABCжаЃЌAB=ACЃЌЩфЯпBPДгBAЫљдкЮЛжУПЊЪМШЦЕуBЫГЪБеыа§зЊЃЌа§зЊНЧЮЊІСЃЈ0ЁуЃМІСЃМ180ЁуЃЉ
ЃЈ1ЃЉЕБЁЯBAC=60ЁуЪБЃЌНЋBPа§зЊЕНЭМ2ЮЛжУЃЌЕуDдкЩфЯпBPЩЯЃЎШєЁЯCDP=120ЁуЃЌдђЁЯACD ЁЯABDЃЈЬюЁАЃОЁБЁЂЁА=ЁБЁЂЁАЃМЁБЃЉЃЌЯпЖЮBDЁЂCDгыADжЎМфЕФЪ§СПЙиЯЕЪЧ ЃЛ
ЃЈ2ЃЉЕБЁЯBAC=120ЁуЪБЃЌНЋBPа§зЊЕНЭМ3ЮЛжУЃЌЕуDдкЩфЯпBPЩЯЃЌШєЁЯCDP=60ЁуЃЌЧѓжЄЃКBDЉCD=![]() ADЃЛ
ADЃЛ
ЃЈ3ЃЉНЋЭМ3жаЕФBPМЬаја§зЊЃЌЕБ30ЁуЃМІСЃМ180ЁуЪБЃЌЕуDЪЧжБЯпBPЩЯвЛЕуЃЈЕуPВЛдкЯпЖЮBDЩЯЃЉЃЌШєЁЯCDP=120ЁуЃЌЧыжБНгаДГіЯпЖЮBDЁЂCDгыADжЎМфЕФЪ§СПЙиЯЕЃЈВЛБижЄУїЃЉЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊЁбO1ЁЂЁбO2ЕФАыОЖЗжБ№ЮЊ3cmЁЂ5cmЃЌЧвЫќУЧЕФдВаФОрЮЊ8cmЃЌдђЁбO1гыЁбO2ЕФЮЛжУЙиЯЕЪЧЃЈ ЃЉ
A.ЭтЧа
B.ЯрНЛ
C.ФкЧа
D.ФкКЌ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПВЛЪєгкжааФЖдГЦЭМаЮЕФЪЧЃЈЁЁЁЁЃЉ
A.ГЄЗНаЮB.ЦНааЫФБпаЮ
C.ЕШбќжБНЧШ§НЧаЮD.ЯпЖЮ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПдкЦЕЪ§ЗжВМжБЗНЭМжаЃЌга11ИіаЁГЄЗНаЮЃЌШєжаМфвЛИіаЁГЄЗНаЮЕФУцЛ§ЕШгкЦфЫќ10ИіаЁГЄЗНаЮУцЛ§ЕФКЭЕФ ![]() ЃЌЧвЪ§Онга160ИіЃЌдђжаМфвЛзщЕФЦЕЪ§ЮЊЃЈ ЃЉ
ЃЌЧвЪ§Онга160ИіЃЌдђжаМфвЛзщЕФЦЕЪ§ЮЊЃЈ ЃЉ
A.32
B.0.2
C.40
D.0.25
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЙигкСтаЮЕФаджЪЃЌЯТСаа№ЪіВЛе§ШЗЕФЪЧЃЈЁЁЁЁЃЉ
A.СтаЮЕФЫФЬѕБпЖМЯрЕШB.СтаЮЕФЫФИіНЧЖМЯрЕШ
C.СтаЮЕФЖдНЧЯпЛЅЯрДЙжБD.СтаЮЕФЖдНЧЯпЛЅЯрЦНЗж
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМ1ЃЌдке§ЗНаЮABCDЕФЭтВрЃЌзїСНИіЕШБпШ§НЧаЮADEКЭDCFЃЌСЌНгAFЃЌBEЃЎ
ЃЈ1ЃЉЧыХаЖЯЃКAFгыBEЕФЪ§СПЙиЯЕЪЧ ЃЌЮЛжУЙиЯЕЪЧ ЃЛ
ЃЈ2ЃЉШчЭМ2ЃЌШєНЋЬѕМўЁАСНИіЕШБпШ§НЧаЮADEКЭDCFЁББфЮЊЁАСНИіЕШбќШ§НЧаЮADEКЭDCFЃЌЧвEA=ED=FD=FCЁБЃЌЕкЃЈ1ЃЉЮЪжаЕФНсТлЪЧЗёШдШЛГЩСЂЃПЧызїГіХаЖЯВЂИјгшЫЕУїЃЛ
ЃЈ3ЃЉШєШ§НЧаЮADEКЭDCFЮЊвЛАуШ§НЧаЮЃЌЧвAE=DFЃЌED=FCЃЌЕкЃЈ1ЃЉЮЪжаЕФНсТлЖМФмГЩСЂТ№ЃПЧыжБНгаДГіФуЕФХаЖЯЃЎ

ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com