
����Ŀ�����⣺��ͼ��1������Rt��ACB�У���ACB=90����AC=CB����DCE=45������̽��AD��DE��EB����ĵ�����ϵ��
[̽������]
С��ͬѧ����ͼ�α任������CAD�Ƶ�C��ʱ����ת90���õ���CBH������EH������֪��������EBH=90������ECH=��ECB+��BCH=��ECB+��ACD=45�������ݡ��߽DZߡ�����֤��CEH�� ����EH=ED��
��Rt��HBE�У��� �������ɵ�BH2+EB2=EH2����BH=AD���ɵ�AD��DE��EB֮��ĵ�����ϵ�� ��
[ʵ������]
��1����ͼ��2������������ABCD�У���AEF�Ķ���E��F�ֱ���BC��CD���ϣ���AG�������εı߳���ȣ�����EAF�Ķ�����
��2���ڣ�1�������£�����BD���ֱ�AE��AF�ڵ�M��N����BE=2��DF=3��BM=2![]() ������С��ͬѧ̽���Ľ��ۣ��������εı߳���MN�ij���
������С��ͬѧ̽���Ľ��ۣ��������εı߳���MN�ij���
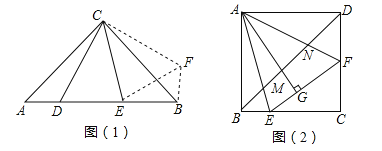
���𰸡�[̽������]��CDE�����ɣ�![]() ��[ʵ������]��1��45������2�������α߳�Ϊ6��MN=
��[ʵ������]��1��45������2�������α߳�Ϊ6��MN=![]() ��
��
��������
�����������1���������ε����ʺ�ȫ�������ε��ж�������֤��Rt��ABE��Rt��AGE��Rt��ADF��Rt��AGF����ȫ�������ε����ʼ��������EAF�Ķ�����
��2���ɣ�1��֪��Rt��ABE��Rt��AGE��Rt��ADF��Rt��AGF����AG=x����CE=x��2��CF=x��3����Ϊ![]() ���õ�
���õ�![]() ����������̣����x��ֵ���ɵõ�AG=6���ڣ�2���У�MN2=MB2+ND2��MN=a��
����������̣����x��ֵ���ɵõ�AG=6���ڣ�2���У�MN2=MB2+ND2��MN=a��![]() �����a��ֵ���������MN�ij���
�����a��ֵ���������MN�ij���
������������ݡ��߽DZߡ�����֤��CEH�ա�CDE����EH=ED����Rt��HBE�У��ɹ��ɶ������ɵ�![]() ����BH=AD���ɵ�AD��DE��EB֮��ĵ�����ϵ��
����BH=AD���ɵ�AD��DE��EB֮��ĵ�����ϵ��![]() ���ʴ�Ϊ����CDE�����ɣ�
���ʴ�Ϊ����CDE�����ɣ�![]() ��
��
��1����Rt��ABE��Rt��AGE�У���AB=AG��AE=AE����Rt��ABE��Rt��AGE��HL�������BAE=��GAE��ͬ����Rt��ADF��Rt��AGF�����GAF=��DAF�����ı���ABCD�������Σ����BAD=90�㣬���EAF=![]() ��BAD=45�㣻
��BAD=45�㣻
��2���ɣ�1��֪��Rt��ABE��Rt��AGE��Rt��ADF��Rt��AGF����BE=EG=2��DF=FG=3����EF=5����AG=x����CE=x��2��CF=x��3����![]() ����
����![]() ����������̣���x=6��x=��1����ȥ������AG=6����BD=
����������̣���x=6��x=��1����ȥ������AG=6����BD=![]() =
=![]() =
=![]() ����AB=6����
����AB=6����![]() ����MN=a����
����MN=a����![]() ������a=
������a=![]() ����MN=
����MN=![]() ��
��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����и�ʽ�У����������ǣ�������
A.cos60����2sin30��B.sin15����cos75��
C.tan30��tan60����1D.sin230��+cos230����1
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪�ı���ABCD�������Σ�����ֱ����AEF��ֱ�Ƕ���E��ֱ��BC�ϣ������B��C�غϣ���FM��AD��������AD�ڵ�M��
��1������E�ڱ�BC�ϣ���M�ڱ�AD���ӳ�����ʱ����ͼ�٣���֤��AB+BE=AM��
����ʾ���ӳ�MF������BC���ӳ����ڵ�H����
��2������E�ڱ�CB���ӳ����ϣ���M�ڱ�AD��ʱ����ͼ�ڣ�����E�ڱ�BC���ӳ����ϣ���M�ڱ�AD��ʱ����ͼ�ۣ���ֱ�д���߶�AB��BE��AM֮���������ϵ������Ҫ֤����
��3���ڣ�1������2���������£���BE=![]() ����AFM=15�㣬��AM= ��
����AFM=15�㣬��AM= ��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪������ABCD��PΪ����AB�ϵ�һ�㣬��BPΪ����������BPEF��ʹ��F���߶�CB���ӳ����ϣ�����EA��EC��

��1����ͼ1������P���߶�AB���ӳ����ϣ���֤��EA=EC��
��2������P���߶�AB�ϣ�
����ͼ2������AC����PΪAB���е�ʱ���жϡ�ACE����״����˵�����ɣ�
����ͼ3����AB=a��BP=b����EPƽ�֡�AECʱ����a��b����AEC�Ķ�����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����������ĶԳ�ͼ�ε��ǣ�������
A.������B.ƽ���ı���
C.����ֱ��������D.�߶�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪�����ϵ�A��ʾ����Ϊ-6����B��������A���Ҳ࣬��AB=14������M�ӵ�A��������ÿ��5����λ���ȵ��ٶ����������������˶������˶�ʱ��Ϊt(t>O)�룮![]()
��1��д�������ϵ�B��ʾ���� �� ��M��ʾ���� (�ú�t��ʽ�ӱ�ʾ)��
��2������N�ӵ�B��������ÿ��3����λ���ȵ��ٶ����������������˶�������M��Nͬʱ�������ʵ�M�˶�������ʱ�ϵ�N?
��3����PΪAM���е㣬FΪMB���е㣬��M���˶������У��߶�_PF�ij����Ƿ����仯?���仯����˵�����ɣ������䣬������߶�PF�ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
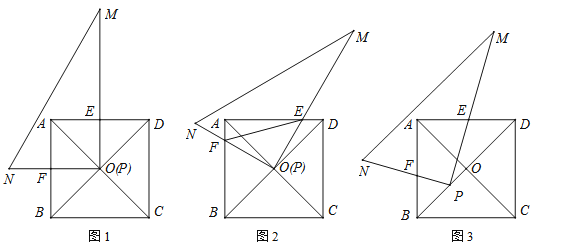
����Ŀ����������ABCD�У��Խ���AC��BD���ڵ�O����Rt��PMN�У���MPN=90����
��1����ͼ1������P���O�غ���PM��AD��PN��AB���ֱ�AD��AB�ڵ�E��F����ֱ��д��PE��PF��������ϵ��
��2����ͼ1�е�Rt��PMN�Ƶ�O˳ʱ����ת�Ƕ�����0��������45������
����ͼ2������ת�����У�1���еĽ�����Ȼ����������������֤����������������˵�����ɣ�
����ͼ2������ת�����У�����DOM=15��ʱ������EF���������εı߳�Ϊ2����ֱ��д���߶�EF�ij���
����ͼ3����ת����Rt��PMN�Ķ���P���߶�OB���ƶ��������O��B�غϣ�����BD=3BPʱ�������ʱPE��PF��������ϵ��������֤������BD=mBPʱ����ֱ��д��PE��PF��������ϵ��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com