
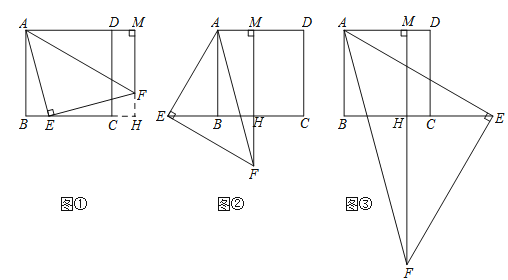
【题目】已知四边形ABCD是正方形,等腰直角△AEF的直角顶点E在直线BC上(不与点B,C重合),FM⊥AD,交射线AD于点M.
(1)当点E在边BC上,点M在边AD的延长线上时,如图①,求证:AB+BE=AM;
(提示:延长MF,交边BC的延长线于点H.)
(2)当点E在边CB的延长线上,点M在边AD上时,如图②;当点E在边BC的延长线上,点M在边AD上时,如图③.请分别写出线段AB,BE,AM之间的数量关系,不需要证明;
(3)在(1),(2)的条件下,若BE=![]() ,∠AFM=15°,则AM= .
,∠AFM=15°,则AM= .

【答案】(1)证明见试题解析;(2)BE= AM+AB;(3)![]() 或
或![]() .
.
【解析】
试题分析:(1)由等腰直角三角形的性质和正方形的性质得到AE=EF,∠ABE=∠EHF=90°,得到△ABE≌△EHF,即可得到结论;
(2)同(1)先证明△ABE≌△EHF,再利用全等三角形的性质定理可得结论;
(3)分三种情况讨论,首先由∠AFM=15°,易得∠EFH,由△ABE≌△EHF,根据全等三角形的性质易得∠AEB,利用锐角三角函数易得AB,利用(1)(2)的结论,易得AM.
试题解析:(1)如图①,延长MF,交边BC的延长线于点H,∵四边形ABCD是正方形,FM⊥AD,∴∠ABE=90°,∠EHF=90°,四边形ABHM为矩形,∴AM=BH=BE+EH
∵△AEF为等腰直角三角形,∴AE=AF,∠AEB+∠FEH=90°,∵∠EFH+∠FEH=90°,∴∠AEB=∠EFH,在△ABE与△EHF中,∵∠ABE=∠EHF=90°,∠ABE=∠EHF=90°,∠AEB=∠EFH,AE=EF,∴△ABE≌△EHF(AAS),∴AB=EH,∵AM=BH=BE+EH,∴AM=BE+AB,即AB+BE=AM;
(2)BE= AM+AB.理由如下:
如图②,∵∠AEB+∠FEH=90°,∠AEB+∠EAB=90°,∴∠FEH=∠EAB,在△ABE与△EHF中,∵∠ABE=∠EHF,∠EAB=∠FEH,AE=FE,∴△ABE≌△EHF(AAS),∴AB=EH=EB+AM;
如图③∠BAE+∠AEB=90°,∠AEB+∠HEF=90°,∴∠BAE=∠HEF,在△ABE与△EHF中,∵∠ABE=∠EHF,∠BAE=∠HEF,AE=FE,∴△ABE≌△EHF(AAS),∴AB=EH,∴BE=BH+EH=AM+AB;
(3)如图①,∵∠AFM=15°,∠AFE=45°,∴∠EFM=60°,∴∠EFH=120°,在△EFH中,∵∠FHE=90°,∠EFH=120°,∴此情况不存在;
如图②,∵∠AFM=15°,∠AFE=45°,∴∠EFH=60°,∵△ABE≌△EHF,∴∠EAB=∠EFH=60°,∵BE=![]() ,∴AB=BEtan60°=
,∴AB=BEtan60°=![]() =3,∵AB=EB+AM,∴AM=AB﹣EB=
=3,∵AB=EB+AM,∴AM=AB﹣EB=![]() ;
;
如图③,∵∠AFM=15°,∠AFE=45°,∴∠EFH=45°﹣15°=30°,∴∠AEB=30°,∵BE=![]() ,∴AB=BEtan30°=
,∴AB=BEtan30°=![]() =1,∵BE=AM+AB,AM=BE﹣AB=
=1,∵BE=AM+AB,AM=BE﹣AB=![]() ,故答案为:
,故答案为:![]() 或
或![]() .
.


 英语小英雄天天默写系列答案
英语小英雄天天默写系列答案 暑假作业安徽少年儿童出版社系列答案
暑假作业安徽少年儿童出版社系列答案科目:初中数学 来源: 题型:
【题目】下列计算正确的是( )
A. (a+2)(a﹣2)=a2﹣2 B. (a+1)(a﹣2)=a2+a﹣2
C. (a+b)2=a2+b2 D. (a﹣b)2=a2﹣2ab+b2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在△ABC中,∠ACB=90°,AC=BC,∠EAC=90°,点M为射线AE上任意一点(不与A重合),连接CM,将线段CM绕点C按顺时针方向旋转90°得到线段CN,直线NB分别交直线CM、射线AE于点F、D.
(1)直接写出∠NDE的度数;
(2)如图2、图3,当∠EAC为锐角或钝角时,其他条件不变,(1)中的结论是否发生变化?如果不变,选取其中一种情况加以证明;如果变化,请说明理由;
(3)如图4,若∠EAC=15°,∠ACM=60°,直线CM与AB交于G,BD=![]() ,其他条件不变,求线段AM的长.
,其他条件不变,求线段AM的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】等腰△ABC的底边BC=8cm,腰长AB=5cm,一动点P在底边上从点B开始向点C以0.25cm/秒的速度运动,当点P运动到PA与腰垂直的位置时,点P运动的时间应为_____秒.
查看答案和解析>>
科目:初中数学 来源: 题型:
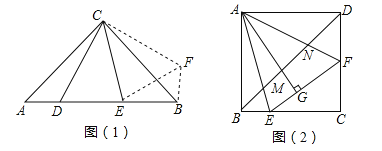
【题目】问题:如图(1),在Rt△ACB中,∠ACB=90°,AC=CB,∠DCE=45°,试探究AD、DE、EB满足的等量关系.
[探究发现]
小聪同学利用图形变换,将△CAD绕点C逆时针旋转90°得到△CBH,连接EH,由已知条件易得∠EBH=90°,∠ECH=∠ECB+∠BCH=∠ECB+∠ACD=45°.根据“边角边”,可证△CEH≌ ,得EH=ED.
在Rt△HBE中,由 定理,可得BH2+EB2=EH2,由BH=AD,可得AD、DE、EB之间的等量关系是 .
[实践运用]
(1)如图(2),在正方形ABCD中,△AEF的顶点E、F分别在BC、CD边上,高AG与正方形的边长相等,求∠EAF的度数;
(2)在(1)条件下,连接BD,分别交AE、AF于点M、N,若BE=2,DF=3,BM=2![]() ,运用小聪同学探究的结论,求正方形的边长及MN的长.
,运用小聪同学探究的结论,求正方形的边长及MN的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com