
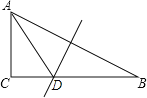
【题目】如图,Rt△ABC中,∠C=90°,BC=15,斜边AB的垂直平分线与∠CAB的平分线都交BC于D点,则点D到斜边AB的距离为___________.
【答案】5
【解析】
根据线段垂直平分线上的点到线段两端点的距离相等可得AD=BD,根据等边对等角的性质可得∠B=∠BAD,再根据三角形内角和定理列式求出∠B=30°,设AB的垂直平分线与AB相交于点E,根据角平分线上的点到角的两边的距离相等可得DE=CD,根据直角三角形30°角所对的直角边等于斜边的一半可得BD=2DE,然后根据BC=CD+BD列式计算即可得解.
如图,
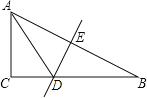
∵斜边AB的垂直平分线与BC相交于D点,
∴AD=BD,
∴∠B=∠BAD,
∵AD是∠BAC的角平分线,
∴∠BAD=∠CAD,
∵∠C=90°,
∴∠B+∠BAD+∠CAD=90°,
即3∠B=90°,
∴∠B=30°,
∴BD=2DE,
∵BC=15,
∴CD+BD=DE+BD=DE+2DE=3DE=15,
∴DE=5,
即点D到斜边AB的距离为5.
故答案为:5.


 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案科目:初中数学 来源: 题型:
【题目】盒中有x个黑球和y个白球,这些球除颜色外无其他差别.若从盒中随机取一个球,它是黑球的概率是 ![]() ;若往盒中再放进1个黑球,这时取得黑球的概率变为
;若往盒中再放进1个黑球,这时取得黑球的概率变为 ![]() .
.
(1)填空:x= , y=;
(2)小王和小林利用x个黑球和y个白球进行摸球游戏.约定:从盒中随机摸取一个,接着从剩下的球中再随机摸取一个,若两球颜色相同则小王胜,若颜色不同则小林胜.求两个人获胜的概率各是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,有一圆柱,其高为12cm,它的底面半径为3cm,在圆柱下底面A处有一只蚂蚁,它想得到上面B处的食物,则蚂蚁经过的最短距离为_________.(π取3)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点A(1,6)和点M(m,n)都在反比例函数y= ![]() (x>0)的图象上,
(x>0)的图象上,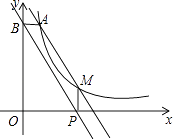
(1)k的值为;
(2)当m=3,求直线AM的解析式;
(3)当m>1时,过点M作MP⊥x轴,垂足为P,过点A作AB⊥y轴,垂足为B,试判断直线BP与直线AM的位置关系,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在□ABCD中,CE![]() AD于点E,且CB=CE,点F为CD边上的一点,CB=CF,连接BF交CE于点G.
AD于点E,且CB=CE,点F为CD边上的一点,CB=CF,连接BF交CE于点G.
(1)若![]() ,CF=
,CF=![]() ,求CG的长;
,求CG的长;
(2)求证:AB=ED+CG

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,OA=OB,点P为△ABO的角平分线的交点,若PN⊥PA交x轴于N,延长OP交AB于M,写出AO,ON,PM之间的数量关系,并证明之.
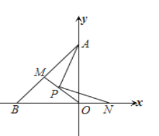
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知正方形ABCD,顶点A(1,3)、B(1,1)、C(3,1),规定“把正方形ABCD先沿x轴翻折,再向左平移1个单位”为一次交换,如此这样,连续经过2016次变换后,正方形ABCD的对角线交点M的坐标变为 . 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】李明从市场上买回一块矩形铁皮,他将此矩形铁皮的四个角各剪去一个边长为1米的正方形后,剩下的部分刚好能围成一个容积为15立方米的无盖长方体运输箱,且此长方体运输箱底面的长比宽多2米,现已知购买这种铁皮每平方米需20元,问购买这张矩形铁皮共花了多少钱?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com