
【题目】如图所示,△A′B′C′是△ABC经过平移得到的,△ABC中任意一点P(x1,y1)平移后的对应点为P′(x1+6,y1+4)。
(1)请写出三角形ABC平移的过程;
(2)分别写出点A′,B′,C′ 的坐标。
(3)求△A′B′C′的面积。
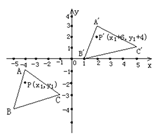
【答案】(1)见解析;(2)A′(2,3) B′(1,0) C′(5,1);(3)5.5
【解析】整体分析:
(1)由x1+6-x1=6,y1+4-y1=4得平移规律;(2)根据(1)中的平移规律即可得到点A′,B′,C′的坐标;(3)把△A′B′C′补形为一个长方形后,利用面积的和差关系求△A′B′C′的面积.
解:(1) △ABC先向右平移6个单位,再向上平移4个单位得到△A′B′C′或△ABC先向上平移4个单位,再向右平移6个单位得到△A′B′C′
(2) A′(2,3) B′(1,0) C′(5,1)
(3)S△A′B′C′=4×3![]() ×3×1
×3×1![]() ×3×2
×3×2![]() ×1×4=121.532=5.5,
×1×4=121.532=5.5,


科目:初中数学 来源: 题型:
【题目】平面直角坐标系中,△ABC的三个顶点坐标分别为A(0,4),B(2,4),C(3,﹣1).
(1)试在平面直角坐标系中,标出A,B,C三点; 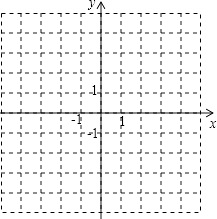
(2)求△ABC的面积.
(3)若△A1B1C1与△ABC关于x轴对称,写出A1、B1、C1的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知直线m∥n,点C是直线m上一点,点D是直线n上一点,CD与直线m、n不垂直,点P为线段CD的中点.
(1)操作发现:直线l⊥m,l⊥n,垂足分别为A、B,当点A与点C重合时(如图①所示),连接PB,请直接写出线段PA与PB的数量关系: .
(2)猜想证明:在图①的情况下,把直线l向上平移到如图②的位置,试问(1)中的PA与PB的关系式是否仍然成立?若成立,请证明;若不成立,请说明理由.
(3)延伸探究:在图②的情况下,把直线l绕点A旋转,使得∠APB=90°(如图③所示),若两平行线m、n之间的距离为2k.求证:PAPB=kAB.

查看答案和解析>>
科目:初中数学 来源: 题型:
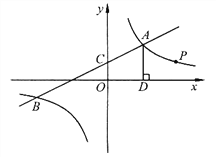
【题目】如图,一次函数![]() 与反比例函数
与反比例函数![]() 的图象交于点
的图象交于点![]() 和
和![]() ,与y轴交于点C.
,与y轴交于点C.
(1)m= , ![]() = ;
= ;
(2)当x的取值是 时, ![]() >
>![]() ;
;
(3)过点A作AD⊥x轴于点D,点P是反比例函数在第一象限的图象上一点.设直线OP与线段AD交于点E,当![]() :
: ![]() =3:1时,求点P的坐标.
=3:1时,求点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
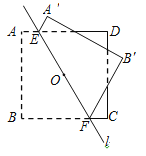
【题目】如图,正方形ABCD的边长为2,点O是正方形的中心,过点O作一条直线l分别交正方形AD,BC两边于点E,F.直线l将正方形分成两部分,将其中的一个部分沿这条直线翻折到另一个部分上,若AE=![]() ,则两个部分图形中不重叠部分的面积为_______.
,则两个部分图形中不重叠部分的面积为_______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一次中学生田径运动会上,根据参加男子跳高初赛的运动员的成绩(单位:m),绘制出如下两幅统计图.请根据相关信息,解答下列问题:
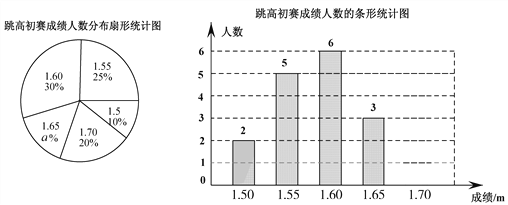
(1)扇形统计图中,初赛成绩为1.65m所在扇形图形的圆心角为_ _°;
(2)补全条形统计图;
(3)这组初赛成绩的中位数是 m;
(4)根据这组初赛成绩确定8人进入复赛,那么初赛成绩为1.60m的运动员杨强能否进入复赛?为什么?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com