
����Ŀ����ֱ֪��m��n����C��ֱ��m��һ�㣬��D��ֱ��n��һ�㣬CD��ֱ��m��n����ֱ����PΪ�߶�CD���е㣮
��1���������֣�ֱ��l��m��l��n������ֱ�ΪA��B������A���C�غ�ʱ����ͼ����ʾ��������PB����ֱ��д���߶�PA��PB��������ϵ���� ����
��2������֤������ͼ�ٵ�����£���ֱ��l����ƽ�Ƶ���ͼ�ڵ�λ�ã����ʣ�1���е�PA��PB�Ĺ�ϵʽ�Ƿ���Ȼ����������������֤����������������˵�����ɣ�
��3������̽������ͼ�ڵ�����£���ֱ��l�Ƶ�A��ת��ʹ�á�APB=90�㣨��ͼ����ʾ��������ƽ����m��n֮��ľ���Ϊ2k����֤��PAPB=kAB��

���𰸡�PA=PB��������PA=PB��
�������������������1������������CBD��ֱ�������Σ����ҵ�PΪ�߶�CD���е㣬Ӧ��ֱ�������ε����ʣ��ɵ�PA=PB���ݴ˽�ɣ���2�����ȹ�C��CE��n�ڵ�E������PE��Ȼ��ֱ��жϳ�PC=PE����PCA=��PEB��AC=BE��Ȼ�����ȫ���������ж��ķ������жϳ���PAC�ס�PBE�������жϳ�PA=PB��Ȼ��������3�������ӳ�AP��ֱ��n�ڵ�F����AE��BD�ڵ�E��Ȼ����������������ж��ķ������жϳ���AEF�ס�BPF�������жϳ�AFBP=AEBF���ٸ�AF=2PA��AE=2k��BF=AB���ɵ�2PAPB=2k��AB������PAPB=kAB���ݴ˽��
�����������1����l��n�� ��BC��BD�� ��������CBD��ֱ�������Σ� ������PΪ�߶�CD���е㣬
��PA=PB��
��ֱ��l����ƽ�Ƶ���ͼ����λ�ã�PA=PB��Ȼ�������������£�
��ͼ������C��CE��n�ڵ�E������PE��
 ��
��
��������CED��ֱ�������Σ���PΪ�߶�CD���е㣬 ��PD=PE�� ������PΪ�߶�CD���е㣬
��PC=PD�� ��PC=PE�� ��PD=PE�� ���CDE=��PEB�� ��ֱ��m��n�� ���CDE=��PCA��
���PCA=��PEB�� ����ֱ��l��m��l��n��CE��m��CE��n�� ��l��CE�� ��AC=BE��
����PAC����PBE�У� ���PAC�ס�PBE�� ��PA=PB��
���PAC�ס�PBE�� ��PA=PB��
��3����ͼ�����ӳ�AP��ֱ��n�ڵ�F����AE��BD�ڵ�E��
 ��
��
��ֱ��m��n�� ��![]() �� ��AP=PF�� �ߡ�APB=90���� ��BP��AF�� ����AP=PF�� ��BF=AB��
�� ��AP=PF�� �ߡ�APB=90���� ��BP��AF�� ����AP=PF�� ��BF=AB��
����AEF����BPF�У�![]() ���AEF�ס�BPF�� ��
���AEF�ס�BPF�� ��![]() �� ��AFBP=AEBF��
�� ��AFBP=AEBF��
��AF=2PA��AE=2k��BF=AB�� ��2PAPB=2k��AB�� ��PAPB=kAB�� ��PA=PB



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ11.3-11����֪DB��AE��B��DC��AF��C����DB=DC����BAC=40�㣬��ADG=130�㣬���DGF=________�� 
A.130��
B.150��
C.100��
D.140��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����и�ʽ�У���x2y��ͬ������ǣ�������
A. xy2B. 2xyC. ��x2yD. 3x2y2
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��Ϊ�˸�������ij��ˮ�ʣ����������������۹�˾��������![]() ̨��ˮ�����豸������
̨��ˮ�����豸������![]() ��
��![]() �����ͺŵ��豸������ÿ̨�ļ۸��´�����ˮ�����±��������飺����һ̨
�����ͺŵ��豸������ÿ̨�ļ۸��´�����ˮ�����±��������飺����һ̨![]() ���豸�ȹ���һ̨
���豸�ȹ���һ̨![]() ���豸��
���豸��![]() ��Ԫ������
��Ԫ������![]() ̨
̨![]() ���豸�ȹ���
���豸�ȹ���![]() ̨
̨![]() ���豸��
���豸��![]() ��Ԫ��
��Ԫ��
|
| |
�۸���Ԫ/̨�� |
|
|
������ˮ������/�£� |
|
|
��![]() ����
����![]() ��
��![]() ��ֵ��
��ֵ��
��![]() ����Ԥ�㣺�����۹�˾������ˮ�����豸���ʽ���
����Ԥ�㣺�����۹�˾������ˮ�����豸���ʽ���![]() ��Ԫ������Ϊ�ù�˾���ļ��ֹ�����
��Ԫ������Ϊ�ù�˾���ļ��ֹ�����
��![]() ���ڣ�
���ڣ�![]() ���ʵ������£���ÿ��Ҫ�����ú�����ˮ��������
���ʵ������£���ÿ��Ҫ�����ú�����ˮ��������![]() �֣�Ϊ�˽�Լ�ʽ�����Ϊ���۹�˾���һ����ʡǮ�Ĺ�����
�֣�Ϊ�˽�Լ�ʽ�����Ϊ���۹�˾���һ����ʡǮ�Ĺ�����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
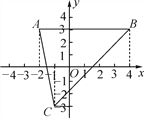
����Ŀ����֪��A(��2��3)��B(4��3)��C(��1����3)��
(1)��A��B����֮��ľ��룻
(2)���C��x��ľ��룻
(3)��������ABC�������
(4)�۲��߶�AB��x��Ĺ�ϵ������D���߶�AB��һ��(����A��B�غ�)�����D��������ʲô�ص㣿
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
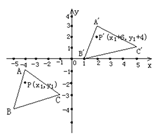
����Ŀ����ͼ��ʾ����A��B��C������ABC����ƽ�Ƶõ��ģ���ABC������һ��P(x1,y1)ƽ�ƺ�Ķ�Ӧ��ΪP��(x1+6��y1+4)��
��1����д��������ABCƽ�ƵĹ��̣�
��2���ֱ�д����A�䣬B�䣬C�� �����ꡣ
��3������A��B��C���������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵ�У�A����1��5����B����1��0����C����4��3���� 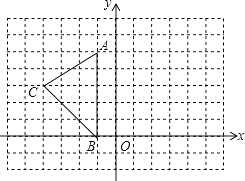
��1���뻭����ABC����y��ԳƵġ�DEF������D��E��F�ֱ���A��B��C�Ķ�Ӧ�㣬��д��������
��2��ֱ��д��D��E��F��������꣺D������E������F������
��3����y���ϴ���һ�㣬ʹPC��PB������P������Ϊ ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���̵깺��һ����Ʒ�������ۣ�����Ϊÿ��40Ԫ���ۼ�Ϊÿ��60Ԫ��ÿ�¿�����300�����г����鷴ӳ�������۸�ʱ���ۼ�ÿ��1Ԫÿ��Ҫ����10�����ۼ�ÿ�½�1Ԫÿ��Ҫ����20����Ϊ�˻�ø���������ֽ���Ʒ�ۼ۵���Ϊ60��x��Ԫ/������x��0���ۼ����ǣ�x��0���ۼ��½�����ÿ����Ʒ����Ϊy��������������Ϊw��Ԫ����
��1��ֱ��д��y��x֮��ĺ�����ϵʽ��
��2�������ۼ۸��Ƕ���ʱ����ʹ������������������ʱ���٣�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����ABC�У�AB=AC����B=����
��1����ͼ1����D��E�ֱ��ڱ�AB��AC�ϣ��߶�DE�Ĵ�ֱƽ����MN��ֱ��BC�ڵ�M����DE�ڵ�N����֤��BD+CE=BC���貹��������EMN= ���ú�����ʽ�ӱ�ʾ������������֤����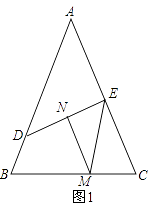
��2���ѣ�1���е�������Ϊ��D��E�ֱ��ڱ�BA��AC�ӳ����ϣ��߶�DE�Ĵ�ֱƽ����MN��ֱ��BC�ڵ�M����DE�ڵ�N����ͼ2����������������EMN=���ú�����ʽ�ӱ�ʾ����ͨ���۲������������߶�BD��CE��BC֮�������������ϵ��������֤����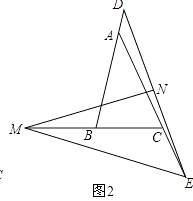
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com