
【题目】商店购进一种商品进行销售,进价为每件40元,售价为每件60元,每月可卖出300件.市场调查反映:调整价格时,售价每涨1元每月要少卖10件;售价每下降1元每月要多卖20件.为了获得更大的利润,现将商品售价调整为60+x(元/件)(x>0即售价上涨,x<0即售价下降),每月商品销量为y(件),月利润为w(元).
(1)直接写出y与x之间的函数关系式;
(2)当销售价格是多少时才能使月利润最大?最大月利润时多少?
【答案】(1)y=![]()
(2)当销售价格为65元时,利润最大,最大利润为6250元.
【解析】试题分析:(1)根据题意售价每涨元每月要少卖件,售价每下降元每月要多卖件,根据等量关系列出方程即可;(2)根据每件商品的利润与商品销量的乘积即为总利润,列出与的函数关系式,再利用二次函数的性质可得到最大利润.
试题解析:
(1)y=![]()
(2)当0≤x≤30时
w=( 20+x )(( 300-10x )=-10x 2+100x+6000=-10( x-5 )2+6250
x=5时,w有最大值为6250
当-20≤x<0时
w=( 20+x )(( 300-20x )=-20x 2-100x+6000=-20( x+ ![]() )2+6125
)2+6125
x=-![]() 时,w有最大值为6125.
时,w有最大值为6125.
由题意知x应取整数,故当x=-2或x=-3时,w<6125<6250
所以,当销售价格为65元时,利润最大,最大利润为6250元.


 53随堂测系列答案
53随堂测系列答案科目:初中数学 来源: 题型:
【题目】已知直线m∥n,点C是直线m上一点,点D是直线n上一点,CD与直线m、n不垂直,点P为线段CD的中点.
(1)操作发现:直线l⊥m,l⊥n,垂足分别为A、B,当点A与点C重合时(如图①所示),连接PB,请直接写出线段PA与PB的数量关系: .
(2)猜想证明:在图①的情况下,把直线l向上平移到如图②的位置,试问(1)中的PA与PB的关系式是否仍然成立?若成立,请证明;若不成立,请说明理由.
(3)延伸探究:在图②的情况下,把直线l绕点A旋转,使得∠APB=90°(如图③所示),若两平行线m、n之间的距离为2k.求证:PAPB=kAB.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD的边长为2,点O是正方形的中心,过点O作一条直线l分别交正方形AD,BC两边于点E,F.直线l将正方形分成两部分,将其中的一个部分沿这条直线翻折到另一个部分上,若AE=![]() ,则两个部分图形中不重叠部分的面积为_______.
,则两个部分图形中不重叠部分的面积为_______.
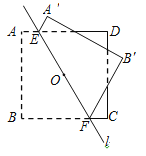
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】利民种子培育基地用A、B、C三种型号的玉米种子共1500粒进行发芽试验,从中选出发芽率高的种子进行推广.通过试验知道,C型号种子的发芽率为80%,根据试验数据绘制了下面两个不完整的统计图(图1、图2):
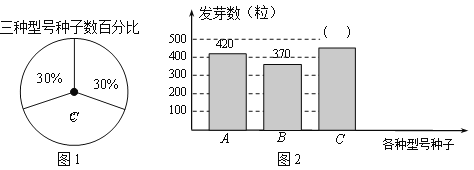
(1)C型号种子的发芽数是_________粒;
(2)直接写出应选哪种型号的种子进行推广?
(3)如果将所有已发芽的种子放到一起,从中随机取出一粒,求取到C型号发芽种子的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,对于任意三点A,B,C,给出如下定义:如果矩形的任何一条边均与某条坐标轴平行,且A,B,C三点都在矩形的内部或边界上,则称该矩形为点A,B,C的覆盖矩形.点A,B,C的所有覆盖矩形中,面积最小的矩形称为点A,B,C的最优覆盖矩形.例如,下图中的矩形A1B1C1D1,A2B2C2D2,AB3C3D3都是点A,B,C的覆盖矩形,其中矩形AB3C3D3是点A,B,C的最优覆盖矩形.

(1)已知A(![]() 2,3),B(5,0),C(
2,3),B(5,0),C(![]() ,
, ![]() 2).
2).
①当![]() 时,点A,B,C的最优覆盖矩形的面积为 ;
时,点A,B,C的最优覆盖矩形的面积为 ;
②若点A,B,C的最优覆盖矩形的面积为40,则t的值为 ;
(2)已知点D(1,1),点E(![]() ,
, ![]() ),其中点E是函数
),其中点E是函数![]() 的图像上一点,⊙P是点O,D,E的一个面积最小的最优覆盖矩形的外接圆,求出⊙P的半径r的取值范围.
的图像上一点,⊙P是点O,D,E的一个面积最小的最优覆盖矩形的外接圆,求出⊙P的半径r的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com