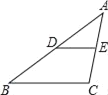
【题目】如图，证明定理：三角形的中位线平行于三角形的第三边，且等于第三边的一半．
已知：点D、E分别是△ABC的边AB、AC的中点．
求证：DE∥BC，DE＝
BC．
目标测试系列答案科目：初中数学 来源： 题型：
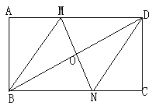
【题目】如图，在矩形ABCD中，对角线BD的垂直平分线MN与AD相交于点N，连接BM，DN.
（1）求证：四边形BMDN是菱形；
（2）若AB=4，AD=8，求MD的长.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，正方形ABCD中，G为BC边上一点，BE⊥AG于E，DF⊥AG于F，连接DE．
（1）求证：△ABE≌△DAF；
（2）若AF=1，四边形ABED的面积为6，求EF的长．
查看答案和解析>>
科目：初中数学 来源： 题型：
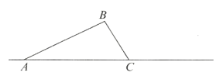
【题目】如图，在三角形
中，
．将三角形绕着点
旋转，使得点
落在直线
上的点
，点
落在点
．
（1）画出旋转后的三角形
．
（2）求线段
在旋转的过程中所扫过的面积（保留
）．
（3）如果在三角形中，
（其中
）．其他条件不变，请你用含有
的代数式，直接写出线段旋转的过程中所扫过的面积（保留）．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】利用勾股定理可以在数轴上画出表示
的点，请依据以下思路完成画图，并保留画图痕迹：
第一步：（计算）尝试满足
，使其中a，b都为正整数.你取的正整数a=____，b=________；
第二步：（画长为
的线段）以第一步中你所取的正整数a，b为两条直角边长画Rt△OEF，使O为原点，点E落在数轴的正半轴上， 
，则斜边OF的长即为
.
请在下面的数轴上画图：（第二步不要求尺规作图，不要求写画法）
第三步：（画表示
的点）在下面的数轴上画出表示
的点M，并描述第三步的画图步骤：_______________________________________________________________.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图1，四边形ABCD是正方形，G是CD边上的一个动点（点G与C、D不重合），以CG为一边在正方形ABCD外作正方形CEFG，连接BG，DE．
（1）①猜想图1中线段BG、线段DE的长度关系及所在直线的位置关系，不必证明；
②将图1中的正方形CEFG绕着点C按顺时针方向旋转任意角度α，得到如图2情形．请你通过观察、测量等方法判断①中得到的结论是否仍然成立，并证明你的判断．
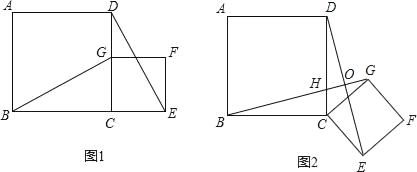
（2）将原题中正方形改为矩形（如图3、4），且AB=a，BC=b，CE=ka，CG=kb （a≠b，k＞0），第（1）题①中得到的结论哪些成立，哪些不成立？若成立，以图4为例简要说明理由．
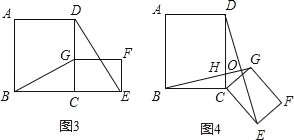
（3）在第（2）题图4中，连接DG、BE，且a=3，b=2，k=
，求BE2+DG2的值．
查看答案和解析>>
科目：初中数学 来源： 题型：
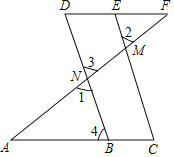
【题目】如图，∠1＝∠2，∠A＝∠F，求证：∠C＝∠D．请阅读下面的解答过程，并填空（理由或数学式）
证明：∵∠1＝∠2（已知）∠1＝∠3（_______）
∴∠2＝∠3（等量代换）
∴BD∥_____（_______）
∴∠4＝_____（_______）
又∵∠A＝∠F（已知）
∴AC∥_____（_______）
∴∠4＝_____（_______）
∴∠C＝∠D（等量代换）
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】某校八年级两个班各选派10名学生参加“垃圾分类知识竞赛，各参赛选手的成绩如下：
八（1）班：88，91，92，93，93，93，94，98，98，100；
八（2）班：89，93，93，93，95，96，96，98，98，99
通过整理，得到数据分析表如下
班级 | 最高分 | 平均分 | 中位数 | 众数 | 方差 |
八（1）班 | 100 |
| 93 | 93 | 12 |
八（2）班 | 99 | 95 |
|
| 8.4 |
（1）求表中
，
，
的值；
（2）依据数据分析表，有同学认为最高分在（1）班，（1）班的成绩比（2）班好．但也有同学认为（2）班的成绩更好．请你写出两条支持八（2）班成绩更好的理由．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
