
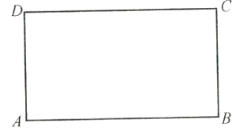
【题目】将长方形纸片向右上方翻折,使得点![]() 和点
和点![]() 重合,画出折痕以及翻折后的图形,折痕与长方形的边
重合,画出折痕以及翻折后的图形,折痕与长方形的边![]() 、
、![]() 分别交于点
分别交于点![]() 、
、![]() ,判断重叠部分图形的形状.
,判断重叠部分图形的形状.
 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案科目:初中数学 来源: 题型:
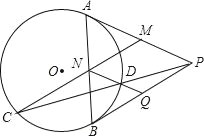
【题目】如图所示,PA、PB为⊙O的切线,M、N是PA、AB的中点,连接MN交⊙O点C,连接PC交⊙O于D,连接ND交PB于Q,求证:MNQP为菱形.
查看答案和解析>>
科目:初中数学 来源: 题型:
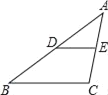
【题目】如图,证明定理:三角形的中位线平行于三角形的第三边,且等于第三边的一半.
已知:点D、E分别是△ABC的边AB、AC的中点.
求证:DE∥BC,DE=![]() BC.
BC.
查看答案和解析>>
科目:初中数学 来源: 题型:
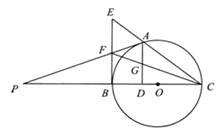
【题目】如图,A是以BC为直径的⊙O上一点,AD⊥BC于点D,过点B作⊙O的切线,与CA的延长线相交于点E,G是AD的中点,连结CG并延长与BE相交于点F,延长AF与CB的延长线相交于点P.
(1)求证:BF=EF:
(2)求证:PA是⊙O的切线;
(3)若FG=BF,且⊙O的半径长为3![]() ,求BD的长度.
,求BD的长度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知A、B两地相距50米,小乌龟从A地出发前往B地,第一次它前进1米,第二次它后退2米,第三次再前进3米,第四次又向后退4米…,按此规律行进,如果A地在数轴上表示的数为﹣16.
![]()
(1)求出B地在数轴上表示的数;
(2)若B地在原点的右侧,经过第七次行进后小乌龟到达点P,第八次行进后到达点Q,点P、点Q到A地的距离相等吗?说明理由?
(3)若B地在原点的右侧,那么经过100次行进后,小乌龟到达的点与点B之间的距离是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)(49)(+91)(5)+(9);
(2)![]()
(3)3x2-[7x-(4x-3)-2x2]
(4)解方程:x+13=5x+37
(5)先化简,再求值:![]() ,其中x=﹣3,y=
,其中x=﹣3,y=![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对于任意有理数a,b,
定义运算:a⊙b=a(a+b)﹣1,等式右边是通常的加法、减法、乘法运算.例如,2⊙5=2(2+5)﹣1=13.
(Ⅰ)求[1⊙(﹣2)]⊙3![]() 的值;
的值;
(Ⅱ)对于任意有理教m,n请你重新定义一种运算“⊕”,使得5⊕3=20,写出你定义的运算:m⊕n=_____.(用含m,n的式子表示)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,以AB为直径作圆O,分别交BC于点D,交CA的延长线于点E,过点D作DH⊥AC于点H,连接DE交线段OA于点F.
(1)求证:DH是圆O的切线;
(2)若A为EH的中点,求![]() 的值;
的值;
(3)若EA=EF=1,求圆O的半径.

查看答案和解析>>
科目:初中数学 来源: 题型:
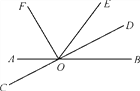
【题目】如图,直线AB与CD相交于点O,OF,OD分别是∠AOE,∠BOE的平分线.
(1)写出∠DOE的补角;
(2)若∠BOE=62°,求∠AOD和∠EOF的度数;
(3)试问射线OD与OF之间有什么特殊的位置关系?为什么?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com