
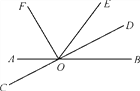
【题目】如图,直线AB与CD相交于点O,OF,OD分别是∠AOE,∠BOE的平分线.
(1)写出∠DOE的补角;
(2)若∠BOE=62°,求∠AOD和∠EOF的度数;
(3)试问射线OD与OF之间有什么特殊的位置关系?为什么?
【答案】(1) ∠COE,∠AOD,∠BOC;(2)∠AOD=149°,∠EOF=59°;(3) 射线OD与OF互相垂直,理由见解析.
【解析】试题分析:(1)根据互补的定义确定∠DOE的补角;
(2)先根据角平分线的定义得出∠BOD的度数,再由邻补角定义可得∠AOD=180°-∠BOD;之后根据邻补角定义可得∠AOE=180°-∠BOE,再由角平分线的定义得出∠EOF的度数;
(3)运用平角的定义和角平分线的定义,证明∠DOF是90°,得直线OD、OF的位置关系.
解:(1)∠DOE的补角为:∠COE,∠AOD,∠BOC.
(2)∵OD是∠BOE的平分线,∠BOE=62°,
∴∠BOD=![]() ∠BOE=31°.
∠BOE=31°.
∴∠AOD=180°-∠BOD=149°.
∴∠AOE=180°-∠BOE=118°.
又∵OF是∠AOE的平分线,
∴∠EOF=![]() ∠AOE=59°.
∠AOE=59°.
(3)射线OD与OF互相垂直.理由如下:
∵OF,OD分别是∠AOE,∠BOE的平分线,
∴∠DOF=∠DOE+∠EOF=![]() ∠BOE+
∠BOE+![]() ∠EOA=
∠EOA=![]() (∠BOE+∠EOA)=
(∠BOE+∠EOA)=![]() ×180°=90°.
×180°=90°.
∴OD⊥OF.


科目:初中数学 来源: 题型:
【题目】图1是由若干个小圆圈堆成的一个形如正三角形的图案,最上面一层有一个圆圈,以下各层均比上一层多一个圆圈,一共堆了n层.将图1倒置后与原图1拼成图2的形状,这样我们可以算出图1中所有圆圈的个数为1+2+3+…+n=![]() .
.
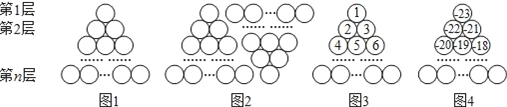
如果图1中的圆圈共有12层,
(1)我们自上往下,在每个圆圈中都按图3的方式填上一串连续的正整数1,2,3,4,…,则最底层最左边这个圆圈中的数是__;
(2)我们自上往下,在每个圆圈中都按图4的方式填上一串连续的整数﹣23,﹣22,﹣21,…,求图4中所有圆圈中各数的绝对值之和.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下列材料:
北京市正围绕着“政治中心、文化中心、国际交往中心、科技创新中心”的定位,深入实施“人文北京、科技北京、绿色北京”的发展战略.“十二五”期间,北京市文化创意产业展现了良好的发展基础和巨大的发展潜力,已经成为首都经济增长的支柱产业.
2011年,北京市文化创意产业实现增加值1938.6亿元,占地区生产总值的12.2%.2012年,北京市文化创意产业继续呈现平稳发展态势,实现产业增加值2189.2亿元,占地区生产总值的12.3%,是第三产业中仅次于金融业、批发和零售业的第三大支柱产业.2013年,北京市文化产业实现增加值2406.7亿元,比上年增长9.1%,文化创意产业作为北京市支柱产业已经排到了第二位.2014年,北京市文化创意产业实现增加值2749.3亿元,占地区生产总值的13.1%,创历史新高,2015年,北京市文化创意产业发展总体平稳,实现产业增加值3072.3亿元,占地区生产总值的13.4%.
根据以上材料解答下列问题:
(1)用折线图将2011﹣2015年北京市文化创意产业实现增加值表示出来,并在图中标明相应数据;
(2)根据绘制的折线图中提供的信息,预估2016年北京市文化创意产业实现增加值约 亿元,你的预估理由 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】观察下列各式:
![]()
![]()
![]()
……
计算:3×(1×2+2×3+3×4+…+99×100)= ( )
A. 97×98×99 B. 98×99×100 C. 99×100×101 D. 100×101×102
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校对七、八、九年级的学生进行体育水平测试,成绩评定为优秀、良好、合格、不合格四个等第.为了解这次测试情况,学校从三个年级随机抽取200名学生的体育成绩进行统计分析.相关数据的统计图、表如下:
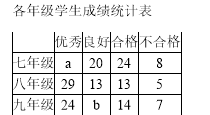
根据以上信息解决下列问题:
(1)在统计表中,a的值为 ,b的值为 ;
(2)在扇形统计图中,八年级所对应的扇形圆心角为 度;
(3)若该校三个年级共有2000名学生参加考试,试估计该校学生体育成绩不合格的人数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】开学初,小明到某商场购物,发现商场正在进行购物返券活动,活动规则如下:购物每满100元,返购物券50元,此购物券在本商场通用,且用购物券购买商品不再返券.小明只购买了单价分别为60元、80元和120元的书包、T恤、运动鞋,在使用购物券参与购买的情况下,他的实际花费为 元.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】证明定理:三角形三条边的垂直平分线相交于一点,并且这一点到三个顶点的距离相等,已知:
如图,在△ABC中,分别作AB边、BC边的垂直平分线,两线相交于点P,分别交AB边、BC边于点E、F.
求证:AB、BC、AC的垂直平分线相交于点P
证明:∵点P是AB边垂直平线上的一点,
∴ = ( ).
同理可得,PB= .
∴ = (等量代换).
∴ (到一条线段两个端点距离相等的点,在这条线段的 )
∴AB、BC、AC的垂直平分线 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com