
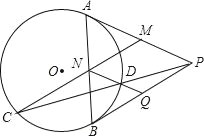
【题目】如图所示,PA、PB为⊙O的切线,M、N是PA、AB的中点,连接MN交⊙O点C,连接PC交⊙O于D,连接ND交PB于Q,求证:MNQP为菱形.
【答案】见解析
【解析】试题分析:连接OA,OB,OC,OD,OP. 由![]() 是
是![]() 的中点,根据三角形中位线的性质,可得MN∥BP.,又由PA、PB为
的中点,根据三角形中位线的性质,可得MN∥BP.,又由PA、PB为![]() 的切线,可得AB⊥OP.可证得NM=MP,然后由射影定理与切割线定理证得O,C,D,N四点共圆,继而证得
的切线,可得AB⊥OP.可证得NM=MP,然后由射影定理与切割线定理证得O,C,D,N四点共圆,继而证得
MP∥NQ,则可得四边形MNQP是平行四边形,证得四边形MNQP是菱形.
试题解析:证明:连接OA,OB,OC,OD,OP.
∵AN=NB,AM=MP.
∴MN∥BP.
∵PA、PB为![]() 的切线,
的切线,
∴AB⊥OP.
∴NM=MP,∠MNP=∠MPN,
在Rt△AOP中,由射影定理,得![]()
由切割线定理,得![]()
∴PNPO=PDPC,
∴O,C,D,N四点共圆,
∴∠PND=∠OCD,∠ONC=∠ODC,
∵OC=OD,
∴∠OCD=∠ODC,
∵∠MNP=∠ONC,
∴∠MNP=∠PND=∠MPN,
∴MP∥NQ,
∴四边形MNQP是平行四边形,
∴四边形MNQP是菱形.


 课时训练江苏人民出版社系列答案
课时训练江苏人民出版社系列答案 黄冈经典趣味课堂系列答案
黄冈经典趣味课堂系列答案 启东小题作业本系列答案
启东小题作业本系列答案科目:初中数学 来源: 题型:
【题目】 观察下列三行数:
2,4,8,16,32,![]()
![]() ,1,2,4,8,
,1,2,4,8,![]()
1,5,7,17,31,![]()
如图,第一行数的第n(n为正整数)个数![]() 用来表示,第二行数的第n个数用
用来表示,第二行数的第n个数用![]() 来表示,第三行数的第n个数用
来表示,第三行数的第n个数用![]() 来表示
来表示
(1)根据你发现的规律,请用含n的代数式表示数![]() ,
,![]() ,
,![]() 的值
的值![]() = ;
= ; ![]() = ;
= ; ![]() = ;
= ;
(2)取每行的第6个数,计算这三个数的和
(3)若![]() 记为x,求
记为x,求![]() (结果用含x的式子表示并化简)
(结果用含x的式子表示并化简)
查看答案和解析>>
科目:初中数学 来源: 题型:
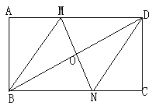
【题目】如图,在矩形ABCD中,对角线BD的垂直平分线MN与AD相交于点N,连接BM,DN.
(1)求证:四边形BMDN是菱形;
(2)若AB=4,AD=8,求MD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知∠AOB=90°,∠BOC=30°,OM平分∠AOC,ON平分∠BOC.
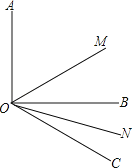
(1)求∠MON的度数;
(2)如果∠AOB=α,其他条件不变,求∠MON的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
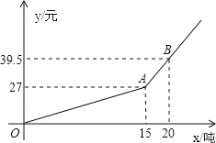
【题目】某市自来水公司为鼓励居民节约用水,采取按月用水量分段收费办法,若某户居民应交交费![]() (元)与用水量
(元)与用水量![]() (吨)的函数关系如图所示。
(吨)的函数关系如图所示。
(1)分别写出当![]() 和
和![]() 时,
时,![]() 与
与![]() 的函数关系式;
的函数关系式;
(2)若某用户该月用水21吨,则应交水费多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
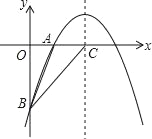
【题目】如图,二次函数y=﹣![]() x2+bx+c的图象经过A(2,0),B(0,﹣6)两点,
x2+bx+c的图象经过A(2,0),B(0,﹣6)两点,
(1)求这个二次函数的解析式;
(2)设该二次函数的对称轴与x轴交于点C,连接BA,BC,求△ABC的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD中,G为BC边上一点,BE⊥AG于E,DF⊥AG于F,连接DE.
(1)求证:△ABE≌△DAF;
(2)若AF=1,四边形ABED的面积为6,求EF的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在三角形![]() 中,
中,![]() .将三角形
.将三角形![]() 绕着点
绕着点![]() 旋转,使得点
旋转,使得点![]() 落在直线
落在直线![]() 上的点
上的点![]() ,点
,点![]() 落在点
落在点![]() .
.
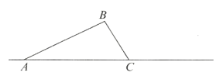
(1)画出旋转后的三角形![]() .
.
(2)求线段![]() 在旋转的过程中所扫过的面积(保留
在旋转的过程中所扫过的面积(保留![]() ).
).
(3)如果在三角形![]() 中,
中,![]() (其中
(其中![]() ).其他条件不变,请你用含有
).其他条件不变,请你用含有![]() 的代数式,直接写出线段
的代数式,直接写出线段![]() 旋转的过程中所扫过的面积(保留
旋转的过程中所扫过的面积(保留![]() ).
).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com