
【题目】如图,已知∠AOB=90°,∠BOC=30°,OM平分∠AOC,ON平分∠BOC.
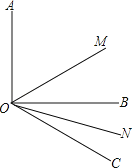
(1)求∠MON的度数;
(2)如果∠AOB=α,其他条件不变,求∠MON的度数.
【答案】(1)45°;(2)![]() α
α
【解析】
(1)先求得∠AOC的度数,然后由角平分线的定义可知∠MOC=60°,∠CON=15°,最后根据∠MON=∠MOC﹣∠CON求解即可;
(2)先求得∠AOC=α+30°,由角平分线的定义可知∠MOC=![]() α+15°,∠CON=15°,最后根据∠MON=∠MOC﹣∠CON求解即可.
α+15°,∠CON=15°,最后根据∠MON=∠MOC﹣∠CON求解即可.
解:(1)∵∠AOB=90°,∠BOC=30°,
∴∠AOC=90°+30=120°.
由角平分线的性质可知:∠MOC=![]() ∠AOC=60°,∠CON=
∠AOC=60°,∠CON=![]() ∠BOC=15°.
∠BOC=15°.
∵∠MON=∠MOC﹣∠CON,
∴∠MON=60°﹣15°=45°;
(2)∵∠AOB=α,∠BOC=30°,
∴∠AOC=α+30°.
由角平分线的性质可知:∠MOC=![]() ∠AOC=
∠AOC=![]() α+15°,∠CON=
α+15°,∠CON=![]() ∠BOC=15°.
∠BOC=15°.
∵∠MON=∠MOC﹣∠CON,
∴∠MON=![]() α+15°﹣15°=
α+15°﹣15°=![]() α.
α.


 开心蛙状元作业系列答案
开心蛙状元作业系列答案 课时掌控随堂练习系列答案
课时掌控随堂练习系列答案 一课一练一本通系列答案
一课一练一本通系列答案科目:初中数学 来源: 题型:
【题目】下面是小东设计的“过直线外一点作这条直线的平行线”的尺规作图过程.已知:如图1,直线l及直线l外一点A.
求作:直线AD,使得AD∥l.作法:如图2,
①在直线l上任取一点B,连接AB;
②以点B为圆心,AB长为半径画弧,
交直线l于点C;
③分别以点A,C为圆心,AB长为半径
画弧,两弧交于点D(不与点B重合);
④作直线AD.
所以直线AD就是所求作的直线.根据小东设计的尺规作图过程,完成下面的证明.(说明:括号里填推理的依据)
证明:连接CD.
∵AD=CD=__________=__________,
∴四边形ABCD是 ( ).
∴AD∥l( ).
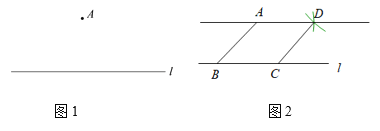
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,一个点从数轴上的原点开始,先向右移动3个单位长度,再向左移动5个单位长度,可以看到终点表示的数是-2,已知点A,B是数轴上的点,请参照图并思考,完成下列各题.
(1)如果点A表示数-3,将点A向右移动7个单位长度,那么终点B表示的数是_____,A,B两点间的距离是_____;
(2)如果点A表示数3,将A点向左移动7个单位长度,再向右移动5个单位长度,那么终点表示的数是_____,A,B两点间的距离为_____;
(3)如果点A表示数-4,将A点向右移动168个单位长度,再向左移动256个单位长度,那么终点B表示的数是_____,A、B两点间的距离是_____;
(4)一般地,如果A点表示的数为m,将A点向右移动n个单位长度,再向左移动p个单位长度,那么请你猜想终点B表示什么数?A,B两点间的距离为多少?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知平面直角坐标系中两定点A(﹣1,0)、B(4,0),抛物线y=ax2+bx﹣2(a≠0)过点A,B,顶点为C,点P(m,n)(n<0)为抛物线上一点.
(1)求抛物线的解析式和顶点C的坐标;
(2)当∠APB为钝角时,求m的取值范围;
(3)若m>![]() ,当∠APB为直角时,将该抛物线向左或向右平移t(0<t<
,当∠APB为直角时,将该抛物线向左或向右平移t(0<t<![]() )个单位,点C、P平移后对应的点分别记为C′、P′,是否存在t,使得首位依次连接A、B、P′、C′所构成的多边形的周长最短?若存在,求t的值并说明抛物线平移的方向;若不存在,请说明理由.
)个单位,点C、P平移后对应的点分别记为C′、P′,是否存在t,使得首位依次连接A、B、P′、C′所构成的多边形的周长最短?若存在,求t的值并说明抛物线平移的方向;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如果一个多位自然数的任意两个相邻数位上,右边数位上的数总比左边数位上数大1,那么我们把这样的自然数叫做“相连数”.例如:234,4567,56789,…都是“相连数”.
(1)请直接写出最大的两位“相连数”与最小的三位“相连数”,并求它们的差.
(2)若某个“相连数”恰好等于其个位数的469倍,求这个“相连数”.
查看答案和解析>>
科目:初中数学 来源: 题型:
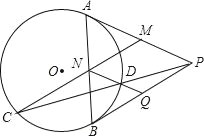
【题目】如图所示,PA、PB为⊙O的切线,M、N是PA、AB的中点,连接MN交⊙O点C,连接PC交⊙O于D,连接ND交PB于Q,求证:MNQP为菱形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,∠AGF=∠ABC,∠ 1+∠ 2=180°.
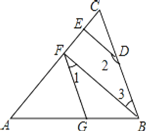
(1)试判断BF与DE的位置关系,并说明理由;
(2)若BF⊥AC,∠CDE=30°,求∠AFG的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
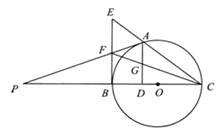
【题目】如图,A是以BC为直径的⊙O上一点,AD⊥BC于点D,过点B作⊙O的切线,与CA的延长线相交于点E,G是AD的中点,连结CG并延长与BE相交于点F,延长AF与CB的延长线相交于点P.
(1)求证:BF=EF:
(2)求证:PA是⊙O的切线;
(3)若FG=BF,且⊙O的半径长为3![]() ,求BD的长度.
,求BD的长度.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com