
【题目】已知平面直角坐标系中两定点A(﹣1,0)、B(4,0),抛物线y=ax2+bx﹣2(a≠0)过点A,B,顶点为C,点P(m,n)(n<0)为抛物线上一点.
(1)求抛物线的解析式和顶点C的坐标;
(2)当∠APB为钝角时,求m的取值范围;
(3)若m>![]() ,当∠APB为直角时,将该抛物线向左或向右平移t(0<t<
,当∠APB为直角时,将该抛物线向左或向右平移t(0<t<![]() )个单位,点C、P平移后对应的点分别记为C′、P′,是否存在t,使得首位依次连接A、B、P′、C′所构成的多边形的周长最短?若存在,求t的值并说明抛物线平移的方向;若不存在,请说明理由.
)个单位,点C、P平移后对应的点分别记为C′、P′,是否存在t,使得首位依次连接A、B、P′、C′所构成的多边形的周长最短?若存在,求t的值并说明抛物线平移的方向;若不存在,请说明理由.
【答案】(1) 抛物线的解析式为:y=![]() x2﹣
x2﹣![]() x﹣2;C(
x﹣2;C( ![]() ,﹣
,﹣![]() ).(2) ﹣1<m<0或3<m<4;(3)
).(2) ﹣1<m<0或3<m<4;(3)![]()
【解析】分析:(1)待定系数法求解析式即可,求得解析式后转换成顶点式即可.
(2)因为AB为直径,所以当抛物线上的点P在⊙C的内部时,满足∠APB为钝角,所以-1<m<0,或3<m<4.
(3)左右平移时,使A′D+DB″最短即可,那么作出点C′关于x轴对称点的坐标为C″,得到直线P″C″的解析式,然后把A点的坐标代入即可.
详解:(1)∵抛物线y=ax2+bx﹣2(a≠0)过点A,B,
∴![]() ,
,
解得: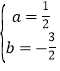 ,
,
∴抛物线的解析式为:y=![]() x2﹣
x2﹣![]() x﹣2;
x﹣2;
∵y=![]() x2﹣
x2﹣![]() x﹣2=
x﹣2=![]() (x﹣
(x﹣![]() )2﹣
)2﹣![]() ,
,
∴C(![]() ,﹣
,﹣![]() ).
).
(2)如图1,以AB为直径作圆M,则抛物线在圆内的部分,能使∠APB为钝角,
∴M(![]() ,0),⊙M的半径=
,0),⊙M的半径=![]() .
.
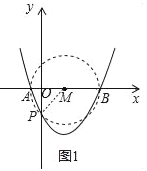
∵P′是抛物线与y轴的交点,
∴OP′=2,
∴MP′=![]() ,
,
∴P′在⊙M上,
∴P′的对称点(3,﹣2),
∴当﹣1<m<0或3<m<4时,∠APB为钝角.
(3)存在;
抛物线向左或向右平移,因为AB、P′C′是定值,所以A、B、P′、C′所构成的多边形的周长最短,只要AC′+BP′最小;
第一种情况:抛物线向右平移,AC′+BP′>AC+BP,
第二种情况:向左平移,如图2所示,由(2)可知P(3,﹣2),
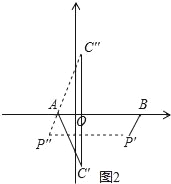
又∵C(![]() ,﹣
,﹣![]() )
)
∴C'(![]() ﹣t,﹣
﹣t,﹣![]() ),P'(3﹣t,﹣2),
),P'(3﹣t,﹣2),
∵AB=5,
∴P″(﹣2﹣t,﹣2),
要使AC′+BP′最短,只要AC′+AP″最短即可,
点C′关于x轴的对称点C″(![]() ﹣t,
﹣t,![]() ),
),
设直线P″C″的解析式为:y=kx+b,
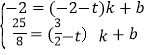 ,
,
解得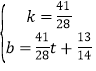
∴直线y=![]() ,
,
当P″、A、C″在一条直线上时,周长最小,
∴![]() =0
=0
∴t=![]() .
.
故将抛物线向左平移![]() 个单位连接A、B、P′、C′所构成的多边形的周长最短.
个单位连接A、B、P′、C′所构成的多边形的周长最短.


 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案科目:初中数学 来源: 题型:
【题目】如图,已知直线l:y=ax+b与反比例函数y=﹣![]() 的图象交于A(﹣4,1)、B(m,﹣4),且直线l与y轴交于点C.
的图象交于A(﹣4,1)、B(m,﹣4),且直线l与y轴交于点C.
(1)求直线l的解析式;
(2)若不等式ax+b>﹣![]() 成立,则x的取值范围是 ;
成立,则x的取值范围是 ;
(3)若直线x=n(n<0)与y轴平行,且与双曲线交于点D,与直线l交于点H,连接OD、OH、OA,当△ODH的面积是△OAC面积的一半时,求n的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
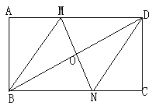
【题目】如图,在矩形ABCD中,对角线BD的垂直平分线MN与AD相交于点N,连接BM,DN.
(1)求证:四边形BMDN是菱形;
(2)若AB=4,AD=8,求MD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,在梯形ABCD中,AB∥CD,∠D=90°,AD=CD=2,点E在边AD上(不与点A、D重合),∠CEB=45°,EB与对角线AC相交于点F,设DE=x.
(1)用含x的代数式表示线段CF的长;
(2)如果把△CAE的周长记作C△CAE,△BAF的周长记作C△BAF,设![]() =y,求y关于x的函数关系式,并写出它的定义域;
=y,求y关于x的函数关系式,并写出它的定义域;
(3)当∠ABE的正切值是![]() 时,求AB的长.
时,求AB的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知∠AOB=90°,∠BOC=30°,OM平分∠AOC,ON平分∠BOC.
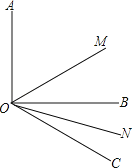
(1)求∠MON的度数;
(2)如果∠AOB=α,其他条件不变,求∠MON的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
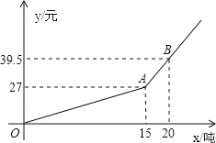
【题目】某市自来水公司为鼓励居民节约用水,采取按月用水量分段收费办法,若某户居民应交交费![]() (元)与用水量
(元)与用水量![]() (吨)的函数关系如图所示。
(吨)的函数关系如图所示。
(1)分别写出当![]() 和
和![]() 时,
时,![]() 与
与![]() 的函数关系式;
的函数关系式;
(2)若某用户该月用水21吨,则应交水费多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD中,G为BC边上一点,BE⊥AG于E,DF⊥AG于F,连接DE.
(1)求证:△ABE≌△DAF;
(2)若AF=1,四边形ABED的面积为6,求EF的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
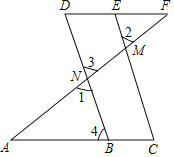
【题目】如图,∠1=∠2,∠A=∠F,求证:∠C=∠D.请阅读下面的解答过程,并填空(理由或数学式)
证明:∵∠1=∠2(已知)∠1=∠3(_______)
∴∠2=∠3(等量代换)
∴BD∥_____(_______)
∴∠4=_____(_______)
又∵∠A=∠F(已知)
∴AC∥_____(_______)
∴∠4=_____(_______)
∴∠C=∠D(等量代换)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com