
����Ŀ����֪A��B�������50�ף�С�ڹ��A�س���ǰ��B�أ���һ����ǰ��1�ף��ڶ���������2�ף���������ǰ��3�ף����Ĵ��������4���������˹����н������A���������ϱ�ʾ����Ϊ��16��
![]()
��1�����B���������ϱ�ʾ������
��2����B����ԭ����Ҳ࣬�������ߴ��н���С�ڹ굽���P���ڰ˴��н����Q����P����Q��A�صľ��������˵�����ɣ�
��3����B����ԭ����Ҳ࣬��ô����100���н���С�ڹ굽��ĵ����B֮��ľ����Ƕ��٣�
���𰸡���1��34��66����2����P����Q��A�صľ�����ȣ����ɼ���������3��С�ڹ굽��ĵ����B֮��ľ�����100�ף�
��������
��1���������ϱ�ʾ-16�ĵ��ƶ�50����λ�����õĵ��ʾΪ-16-50=-66��-16+50=34��
��2�������ϵ���ƶ�������������Ҽ��������ݹ��ɼ��㼴�ɣ�
��3������100Ϊż���ɵ��������ϱ�ʾ�������ٸ��������ľ��빫ʽ������⣮
��1����16+50��34����16��50����66��
��B���������ϱ�ʾ������34��66��
��2�����ߴ��н���![]() ��
��
�ڰ˴��н���![]() ��
��
��Ϊ��P��Q��A��ľ��붼��4�ף�
���Ե�P����Q��A�صľ�����ȣ�
��3����nΪ100ʱ�����������ϱ�ʾ����Ϊ��
![]() ��
��
![]() ���ף���
���ף���
��С�ڹ굽��ĵ����B֮��ľ�����100�ף�



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
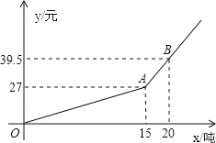
����Ŀ��ij������ˮ��˾Ϊ���������Լ��ˮ,��ȡ������ˮ���ֶ��շѰ취,��ij������Ӧ������![]() (Ԫ)����ˮ��
(Ԫ)����ˮ��![]() (��)�ĺ�����ϵ��ͼ��ʾ��
(��)�ĺ�����ϵ��ͼ��ʾ��
(1)�ֱ�д����![]() ��
��![]() ʱ��
ʱ��![]() ��
��![]() �ĺ�����ϵʽ��
�ĺ�����ϵʽ��
(2)��ij�û�������ˮ21�֣���Ӧ��ˮ�Ѷ���Ԫ?
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����ù��ɶ��������������ϻ�����ʾ![]() �ĵ㣬����������˼·��ɻ�ͼ����������ͼ�ۼ���
�ĵ㣬����������˼·��ɻ�ͼ����������ͼ�ۼ���
��һ���������㣩��������![]() ��ʹ����a��b��Ϊ������.��ȡ��������a=____��b=________��
��ʹ����a��b��Ϊ������.��ȡ��������a=____��b=________��
�ڶ�����������Ϊ![]() ���߶Σ��Ե�һ��������ȡ��������a��bΪ����ֱ�DZ߳���Rt��OEF��ʹOΪԭ�㣬��E����������������ϣ�
���߶Σ��Ե�һ��������ȡ��������a��bΪ����ֱ�DZ߳���Rt��OEF��ʹOΪԭ�㣬��E����������������ϣ� ![]() ����б��OF�ij���Ϊ
����б��OF�ij���Ϊ![]() .
.
��������������ϻ�ͼ�����ڶ�����Ҫ��߹���ͼ����Ҫ��д������
��������������ʾ![]() �ĵ㣩������������ϻ�����ʾ
�ĵ㣩������������ϻ�����ʾ![]() �ĵ�M���������������Ļ�ͼ���裺_______________________________________________________________.
�ĵ�M���������������Ļ�ͼ���裺_______________________________________________________________.
![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
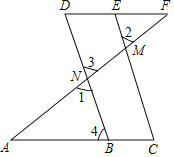
����Ŀ����ͼ����1����2����A����F����֤����C����D�����Ķ�����Ľ����̣�����գ����ɻ���ѧʽ��
֤�����ߡ�1����2����֪����1����3��_______��
���2����3������������
��BD��_____��_______��
���4��_____��_______��
�֡ߡ�A����F����֪��
��AC��_____��_______��
���4��_____��_______��
���C����D������������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��һ���������˶������ָ���![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ������
������ ![]() ���DZ߳�Ϊ
���DZ߳�Ϊ![]() �������Σ�
�������Σ� ![]() ���DZ߳�Ϊ
���DZ߳�Ϊ![]() �������Σ�
��������
��1����ʽ��ʾÿ��![]() �������γ��ص��ܳ�������ʽ�ӻ���
�������γ��ص��ܳ�������ʽ�ӻ���
��2����ʽ��ʾ�����������˶������ܳ�������ʽ�ӻ���
��3�����![]() ��
�� ![]() ���������������˶����������
���������������˶����������

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
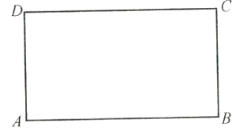
����Ŀ����������ֽƬ�����Ϸ����ۣ�ʹ�õ�![]() �͵�
�͵�![]() �غϣ������ۺ��Լ����ۺ��ͼ�Σ��ۺ��볤���εı�
�غϣ������ۺ��Լ����ۺ��ͼ�Σ��ۺ��볤���εı�![]() ��
��![]() �ֱ��ڵ�
�ֱ��ڵ�![]() ��
��![]() ���ж��ص�����ͼ�ε���״.
���ж��ص�����ͼ�ε���״.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
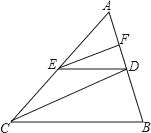
����Ŀ����ͼ������ABC�У�EF��CD��DE��BC��
��1����֤��AF��FD=AD��DB��
��2����AB=15��AD��BD=2��1����DF�ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����A.B����֮��Ĺ�·��Ϊ600ǧ�ף�������A�س������Ŵ˹�·��100ǧ��/Сʱ���ٶ�ǰ��B�أ��������г���B�س����ش˹�·����ǰ��A��.��֪�ұȼ�������1Сʱ���ҳ���4Сʱ�����һ��������������B�غ�����ԭ·ԭ�ٷ���.���ҵڶ����������ʱ�ҹ�������mǧ�ף���m=______.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
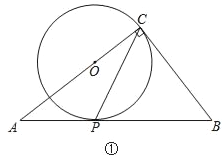
����Ŀ���ڡ�ABC�У���ACB=90����������C�ġ�O��б��AB�����ڵ�P��
��1����ͼ�٣�����O��AC��ʱ����˵��2��ACP=��B��
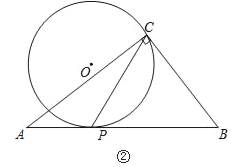
��2����ͼ����AC=8��BC=6������O�ڡ�ABC�ⲿʱ����CP����ȡֵ��Χ��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com