练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】已知连接A.B两地之间的公路长为600千米，甲开车从A地出发沿着此公路以100千米/小时的速度前往B地，乙骑自行车从B地出发沿此公路匀速前往A地.已知乙比甲晚出发1小时，乙出发4小时后与甲第一次相遇，当甲到达B地侯立即原路原速返回.若乙第二次与甲相遇时乙共骑行了m千米，则m=______.

    【答案】

    【解析】

    设乙的速度为x千米/时，根据题意甲乙第一次相遇可列方程，从而求得乙的速度25千米/时，然后再根据题意得到当甲第二次与乙相遇时，可列方程为，从而求得m的值．

    解：设乙的速度为x千米/时，

    ∵乙比甲晚出发1小时，乙出发4小时后与甲第一次相遇

    ∴可得

    解得x=25

    即乙的速度是25千米/时，

    又∵当甲到达B地后立即原路原速返回.若乙第二次与甲相遇时乙共骑行了m千米，

    ∴可得

    解得：

    故答案为：

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】如图，在正方形网格当中，三角形的三个顶点都在格点上．直线与直线相交于点．

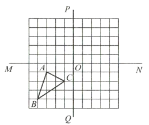
    （1）画出将三角形向右平移5个单位长度后的三角形（点的对应点分别是点）．

    （2）画出三角形关于直线对称的三角形（点的对应点分别是点）．

    （3）画出将三角形绕着点旋转后的三角形（点的对应点分别是点）．

    （4）在三角形，，中，三角形 与三角形 成轴对称，三角形 与三角形 成中心对称

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知A、B两地相距50米，小乌龟从A地出发前往B地，第一次它前进1米，第二次它后退2米，第三次再前进3米，第四次又向后退4米…，按此规律行进，如果A地在数轴上表示的数为﹣16．

    （1）求出B地在数轴上表示的数；

    （2）若B地在原点的右侧，经过第七次行进后小乌龟到达点P，第八次行进后到达点Q，点P、点Q到A地的距离相等吗？说明理由？

    （3）若B地在原点的右侧，那么经过100次行进后，小乌龟到达的点与点B之间的距离是多少？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】对于任意有理数a，b，

    定义运算：a⊙b＝a(a+b)﹣1，等式右边是通常的加法、减法、乘法运算．例如，2⊙5＝2(2+5)﹣1＝13．

    (Ⅰ)求[1⊙(﹣2)]⊙3的值；

    (Ⅱ)对于任意有理教m，n请你重新定义一种运算“⊕”，使得5⊕3＝20，写出你定义的运算：m⊕n＝_____．(用含m，n的式子表示)

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，菱形ABCD的边长为4，∠BAD=120°，点E是AB的中点，点F是AC上的一动点，则EF+BF的最小值是　 　．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在△ABC中，AB=AC，以AB为直径作圆O，分别交BC于点D，交CA的延长线于点E，过点D作DH⊥AC于点H，连接DE交线段OA于点F．

    （1）求证：DH是圆O的切线；

    （2）若A为EH的中点，求的值；

    （3）若EA=EF=1，求圆O的半径．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，四边形ABCD是平行四边形，点E是边CD上的一点，且BC=EC，CF⊥BE交AB于点F，P是EB延长线上一点，下列结论：①BE平分∠CBF；②CF平分∠DCB；③BC=FB；④PF=PC．其中正确的有_____．（填序号）

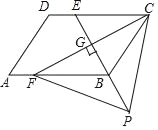
    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图1，关于x的二次函数y=﹣x2+bx+c经过点A（﹣3，0），点C（0，3），点D为二次函数的顶点，DE为二次函数的对称轴，E在x轴上．

    （1）求抛物线的解析式；

    （2）DE上是否存在点P到AD的距离与到x轴的距离相等？若存在求出点P，若不存在请说明理由；

    （3）如图2，DE的左侧抛物线上是否存在点F，使2S△FBC=3S△EBC？若存在求出点F的坐标，若不存在请说明理由．

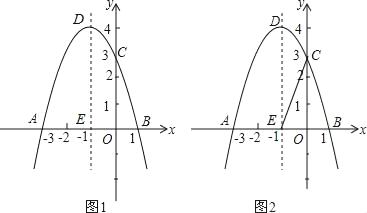
    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知:正方形ABCD，等腰直角三角板的直角顶点落在正方形的顶点D处，使三角板绕点D旋转.

    (1)当三角板旋转到图1的位置时，猜想CE与AF的数量关系，并加以证明；

    (2)在(1)的条件下，若DE:AE:CE= 1: :3，求∠AED的度数；

    (3)若BC= 4，点M是边AB的中点，连结DM，DM与AC交于点O，当三角板的一边DF与边DM重合时(如图2)，若OF=，求CN的长.

    查看答案和解析>>

    同步练习册答案