
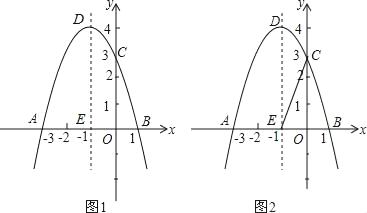
【题目】如图1,关于x的二次函数y=﹣x2+bx+c经过点A(﹣3,0),点C(0,3),点D为二次函数的顶点,DE为二次函数的对称轴,E在x轴上.
(1)求抛物线的解析式;
(2)DE上是否存在点P到AD的距离与到x轴的距离相等?若存在求出点P,若不存在请说明理由;
(3)如图2,DE的左侧抛物线上是否存在点F,使2S△FBC=3S△EBC?若存在求出点F的坐标,若不存在请说明理由.
【答案】(1)y=﹣x2﹣2x+3(2)(﹣1,![]() ﹣1)或(﹣1,﹣
﹣1)或(﹣1,﹣![]() ﹣1);(3)F(
﹣1);(3)F(![]() ,
,![]() )
)
【解析】分析:(1)把A、C两点坐标代入可求得b、c,可求得抛物线解析式;
(2)当点P在∠DAB的平分线上时,过P作PM⊥AD,设出P点坐标,可表示出PM、PE,由角平分线的性质可得到PM=PE,可求得P点坐标;当点P在∠DAB外角平分线上时,同理可求得P点坐标;
(3)可先求得△FBC的面积,过F作FQ⊥x轴,交BC的延长线于Q,可求得FQ的长,可设出F点坐标,表示出B点坐标,从而可表示出FQ的长,可求得F点坐标.
详解:(1)∵二次函数y=﹣x2+bx+c经过点A(﹣3,0),点C(0,3),
∴![]() ,解得
,解得![]() ,
,
∴抛物线的解析式y=﹣x2﹣2x+3,
(2)存在,
当P在∠DAB的平分线上时,如图1,作PM⊥AD,
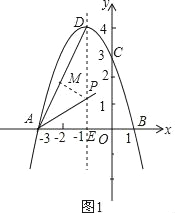
设P(﹣1,m),则PM=PDsin∠ADE=![]() (4﹣m),PE=m,
(4﹣m),PE=m,
∵PM=PE,
∴![]() (4﹣m)=m,m=
(4﹣m)=m,m=![]() ﹣1,
﹣1,
∴P点坐标为(﹣1,![]() ﹣1);
﹣1);
当P在∠DAB的外角平分线上时,如图2,作PN⊥AD,
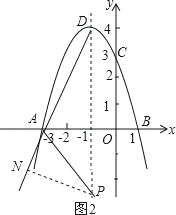
设P(﹣1,n),则PN=PDsin∠ADE=![]() (4﹣n),PE=﹣n,
(4﹣n),PE=﹣n,
∵PN=PE,
∴![]() (4﹣n)=﹣n,n=﹣
(4﹣n)=﹣n,n=﹣![]() ﹣1,
﹣1,
∴P点坐标为(﹣1,﹣![]() ﹣1);
﹣1);
综上可知存在满足条件的P点,其坐标为(﹣1,![]() ﹣1)或(﹣1,﹣
﹣1)或(﹣1,﹣![]() ﹣1);
﹣1);
(3)∵抛物线的解析式y=﹣x2﹣2x+3,
∴B(1,0),
∴S△EBC=![]() EBOC=3,
EBOC=3,
∵2S△FBC=3S△EBC,
∴S△FBC=![]() ,
,
过F作FQ⊥x轴于点H,交BC的延长线于Q,过F作FM⊥y轴于点M,如图3,

∵S△FBC=S△BQH﹣S△BFH﹣S△CFQ=![]() HBHQ﹣
HBHQ﹣![]() BHHF﹣
BHHF﹣![]() QFFM=
QFFM=![]() BH(HQ﹣HF)﹣
BH(HQ﹣HF)﹣![]() QFFM=
QFFM=![]() BHQF﹣
BHQF﹣![]() QFFM=
QFFM=![]() QF(BH﹣FM)=
QF(BH﹣FM)=![]() FQOB=
FQOB=![]() FQ=
FQ=![]() ,
,
∴FQ=9,
∵BC的解析式为y=﹣3x+3,
设F(x0,﹣x02﹣2x0+3),
∴﹣3x0+3+x02+2x0﹣3=9,
解得:x0=![]() 或
或![]() (舍去),
(舍去),
∴点F的坐标是(![]() ,
,![]() ),
),
∵S△ABC=6>![]() ,
,
∴点F不可能在A点下方,
综上可知F点的坐标为(![]() ,
,![]() ).
).


 南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案科目:初中数学 来源: 题型:
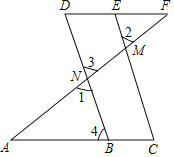
【题目】如图,∠1=∠2,∠A=∠F,求证:∠C=∠D.请阅读下面的解答过程,并填空(理由或数学式)
证明:∵∠1=∠2(已知)∠1=∠3(_______)
∴∠2=∠3(等量代换)
∴BD∥_____(_______)
∴∠4=_____(_______)
又∵∠A=∠F(已知)
∴AC∥_____(_______)
∴∠4=_____(_______)
∴∠C=∠D(等量代换)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知连接A.B两地之间的公路长为600千米,甲开车从A地出发沿着此公路以100千米/小时的速度前往B地,乙骑自行车从B地出发沿此公路匀速前往A地.已知乙比甲晚出发1小时,乙出发4小时后与甲第一次相遇,当甲到达B地侯立即原路原速返回.若乙第二次与甲相遇时乙共骑行了m千米,则m=______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校八年级两个班各选派10名学生参加“垃圾分类知识竞赛,各参赛选手的成绩如下:
八(1)班:88,91,92,93,93,93,94,98,98,100;
八(2)班:89,93,93,93,95,96,96,98,98,99
通过整理,得到数据分析表如下
班级 | 最高分 | 平均分 | 中位数 | 众数 | 方差 |
八(1)班 | 100 |
| 93 | 93 | 12 |
八(2)班 | 99 | 95 |
|
| 8.4 |
(1)求表中![]() ,
,![]() ,
,![]() 的值;
的值;
(2)依据数据分析表,有同学认为最高分在(1)班,(1)班的成绩比(2)班好.但也有同学认为(2)班的成绩更好.请你写出两条支持八(2)班成绩更好的理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
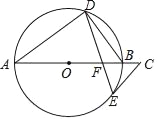
【题目】如图,AB是⊙O的直径,点D,E在⊙O上,∠A=2∠BDE,点C在AB的延长线上,∠C=∠ABD.
(1)求证:CE是⊙O的切线;
(2)若BF=2,EF=![]() ,求⊙O的半径长.
,求⊙O的半径长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,A、B、C分别表示三个村庄,AB=1000米,BC=600米,AC=800米,在社会主义新农村建设中,为了丰富群众生活,拟建一个文化活动中心,要求这三个村庄到活动中心的距离相等,则活动中心P的位置应在( )
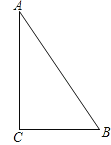
A.AB中点 B.BC中点 C. AC中点 D.∠C的平分线与AB的交点
查看答案和解析>>
科目:初中数学 来源: 题型:
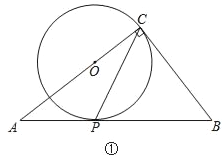
【题目】在△ABC中,∠ACB=90°,经过点C的⊙O与斜边AB相切于点P.
(1)如图①,当点O在AC上时,试说明2∠ACP=∠B;
(2)如图②,AC=8,BC=6,当点O在△ABC外部时,求CP长的取值范围.
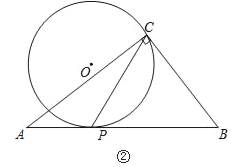
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,菱形ABCD中,∠BAD=60°,AC与BD交于点O,E为CD延长线上的一点,且CD=DE,连接BE,分别交AC、AD于点F、G,连接OG,则下列结论:①OG=![]() AB;②图中与△EGD全等的三角形共有5个;③以点A、B、D、E为项点的四边形是菱形;④S四边形ODGF=S△ABF.其中正确的结论是( )
AB;②图中与△EGD全等的三角形共有5个;③以点A、B、D、E为项点的四边形是菱形;④S四边形ODGF=S△ABF.其中正确的结论是( )
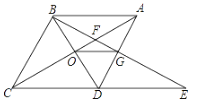
A. ①③B. ①③④C. ①②③D. ②②④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下列材料,完成(1)、(2)小题.在平面直角坐标系中,已知![]() 轴上两点
轴上两点![]() ,
,![]() 的距离记作
的距离记作![]() ,如果
,如果![]() ,
,![]() 是平面上任意两点,我们可以通过构造直角三角形来求
是平面上任意两点,我们可以通过构造直角三角形来求![]() 间的距离,如图1,过点
间的距离,如图1,过点![]() 、
、![]() 分别向
分别向![]() 轴、
轴、![]() 轴作垂线
轴作垂线![]() ,
,![]() 和
和![]() ,
,![]() ,垂足分别是
,垂足分别是![]() ,
,![]() ,
,![]() ,
,![]() ,直线
,直线![]() 交
交![]() 于点
于点![]() ,在
,在![]() 中,
中,![]() ,
,![]() ∴
∴![]() ∴
∴![]() ,我们称此公式
,我们称此公式![]() 为平面直角坐标系内任意两点
为平面直角坐标系内任意两点![]() ,
,![]() 间的距离公式
间的距离公式
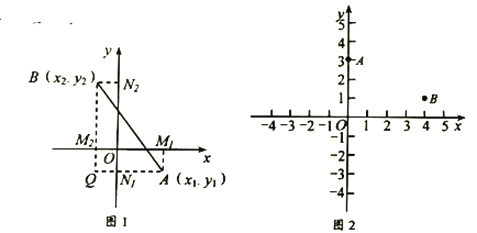
(1)直接应用平面内两点间距离公式计算点![]() ,
,![]() 的距离为_________
的距离为_________
(2)如图2,已知在平面直角坐标系中有两点![]() ,
,![]() ,
,![]() 为
为![]() 轴上任意一点,求
轴上任意一点,求![]() 的最小值
的最小值
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com