
����Ŀ���Ķ����в��ϣ���ɣ�1������2��С��.��ƽ��ֱ������ϵ�У���֪![]() ��������
��������![]() ��
��![]() �ľ������
�ľ������![]() �����
�����![]() ��
��![]() ��ƽ�����������㣬���ǿ���ͨ������ֱ������������
��ƽ�����������㣬���ǿ���ͨ������ֱ������������![]() ��ľ��룬��ͼ1������
��ľ��룬��ͼ1������![]() ��
��![]() �ֱ���
�ֱ���![]() �ᡢ
�ᡢ![]() ��������
��������![]() ��
��![]() ��
��![]() ��
��![]() ������ֱ���
������ֱ���![]() ��
��![]() ��
��![]() ��
��![]() ��ֱ��
��ֱ��![]() ��
��![]() �ڵ�
�ڵ�![]() ����
����![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ,���dzƴ˹�ʽ
,���dzƴ˹�ʽ![]() Ϊƽ��ֱ������ϵ����������
Ϊƽ��ֱ������ϵ����������![]() ��
��![]() ��ľ��빫ʽ
��ľ��빫ʽ
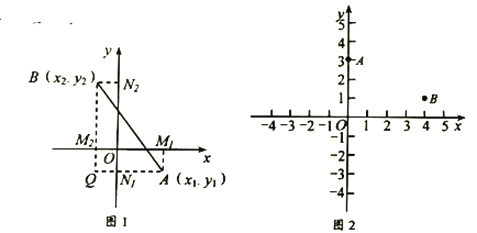
��1��ֱ��Ӧ��ƽ�����������빫ʽ�����![]() ��
��![]() �ľ���Ϊ_________
�ľ���Ϊ_________
��2����ͼ2����֪��ƽ��ֱ������ϵ��������![]() ��
��![]() ��
��![]() Ϊ
Ϊ![]() ��������һ�㣬��
��������һ�㣬��![]() ����Сֵ
����Сֵ

| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
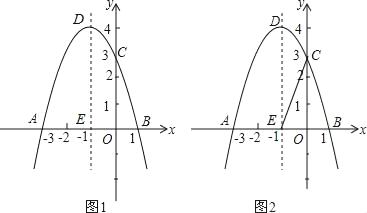
����Ŀ����ͼ1������x�Ķ��κ���y=��x2+bx+c������A����3��0������C��0��3������DΪ���κ����Ķ��㣬DEΪ���κ����ĶԳ��ᣬE��x���ϣ�
��1���������ߵĽ���ʽ��
��2��DE���Ƿ���ڵ�P��AD�ľ����뵽x��ľ�����ȣ������������P������������˵�����ɣ�
��3����ͼ2��DE��������������Ƿ���ڵ�F��ʹ2S��FBC=3S��EBC�������������F�����꣬����������˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪:������ABCD������ֱ�����ǰ��ֱ�Ƕ������������εĶ���D����ʹ���ǰ��Ƶ�D��ת.
(1)�����ǰ���ת��ͼ1��λ��ʱ������CE��AF��������ϵ��������֤����
(2)��(1)�������£���DE:AE:CE= 1: ![]() :3�����AED�Ķ�����
:3�����AED�Ķ�����
(3)��BC= 4����M�DZ�AB���е㣬����DM��DM��AC���ڵ�O�������ǰ��һ��DF���DM�غ�ʱ(��ͼ2)����OF=![]() ����CN�ij�.
����CN�ij�.

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����������ʽ�е�����������ĸ����������ʽ���䣬����������ʽΪ��ȫ�Գ�ʽ����a+b+c������ȫ�Գ�ʽ��������������ʽ���٣�a��b��2����ab+bc+ca����a2b+b2c+c2a����������ȫ�Գ�ʽ���ǣ�������
A. �٢ڢ� B. �٢� C. �ڢ� D. �٢�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����������������Ȼ����ʹABCD��Ϊ���ε��ǣ�������
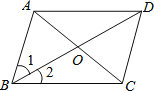
A. AB=BC B. AC��BD C. ��ABC=90�� D. ��1=��2
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��Ϊ�˽ⱾУ���꼶ѧ����ĩ��ѧ���������С���ھ��꼶�����ȡ��һ����ѧ������ĩ��ѧ�ɼ�Ϊ��������ΪA��100��90�֣���B��89��80�֣���C��79��60�֣���D��59��0�֣��ĸ��ȼ�����ͳ�ƣ�����ͳ�ƽ�����Ƴ�����ͳ��ͼ���������ͳ��ͼ����������⣺
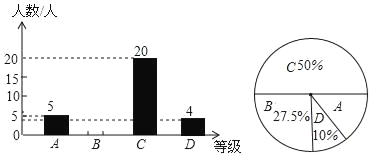
��1����������ȡ��ѧ�����ж����ˣ�
��2���벹ȫ����ͳ��ͼ��
��3�����ѧУ���꼶����ѧ��1200�ˣ�������Ϊ80�֣���80�֣�����Ϊ���㣬�������ξ��꼶ѧ����ĩ��ѧ���Գɼ�Ϊ�����ѧ��������Լ�ж��٣�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������ABCD��MN�ֱ���AB��CD����AM=CN��MN��AC���ڵ�O������BO����DAC=62�㣬���OBC�Ķ���Ϊ��������
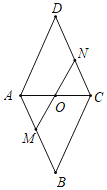
A. 28��B. 52��C. 62��D. 72��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij����̨��һ�������Խ�Ŀ�У�����ϷPK���ڣ�Ϊ�������ѡ��Ϸ˫������Ա�������������������Ϸ���ò����İײ���ס������ɫ������ͬ��ϸ��AA1��BB1��CC1��ֻ¶�����ǵ�ͷ��β����ͼ��ʾ�����ɼס�����λ�α��ֱ�Ӱײ����˸�ѡһ��ϸ������������������ѡ��ͬһ��ϸ����������ͬ�ӣ�����Ϊ������Ա��
��1�����α���������ѡ��һ��ϸ������������ǡ�ó��ϸ��AA1�ĸ��ʣ�
��2�����û���״ͼ�����б�������ס�����λ�α��ܷ�Ϊͬ�ӵĸ��ʣ�
![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��BD����ABC�Ľ�ƽ��������E��F�ֱ���BC��AB������DE��AB��BE=AF��
��1����֤���ı���ADEF��ƽ���ı�����
��2������ABC=60�㣬BD=4����ƽ���ı���ADEF�������
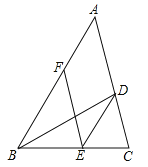
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com