
【题目】如图,在菱形ABCD中MN分别在AB、CD上且AM=CN,MN与AC交于点O,连接BO若∠DAC=62°,则∠OBC的度数为( )
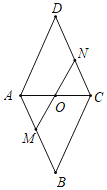
A. 28°B. 52°C. 62°D. 72°
 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
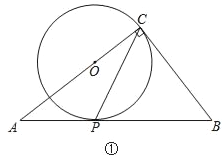
【题目】在△ABC中,∠ACB=90°,经过点C的⊙O与斜边AB相切于点P.
(1)如图①,当点O在AC上时,试说明2∠ACP=∠B;
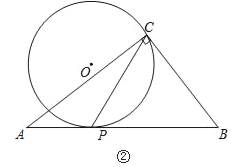
(2)如图②,AC=8,BC=6,当点O在△ABC外部时,求CP长的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】用棋子摆成的“上”字型图案如图所示现察此图案的规律,并回答:
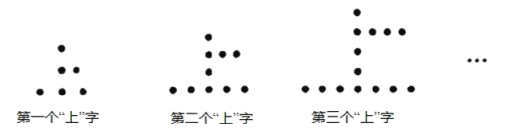
(1)依照此规律,第五个图形中共有 个棋子,第八个图形中共有 个棋子.
(2)第![]() (
(![]() 为正整数)个图形中共有 个棋子.
为正整数)个图形中共有 个棋子.
(3)根据(2)中的结论,第几个图形中有2022个棋子?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下列材料,完成(1)、(2)小题.在平面直角坐标系中,已知![]() 轴上两点
轴上两点![]() ,
,![]() 的距离记作
的距离记作![]() ,如果
,如果![]() ,
,![]() 是平面上任意两点,我们可以通过构造直角三角形来求
是平面上任意两点,我们可以通过构造直角三角形来求![]() 间的距离,如图1,过点
间的距离,如图1,过点![]() 、
、![]() 分别向
分别向![]() 轴、
轴、![]() 轴作垂线
轴作垂线![]() ,
,![]() 和
和![]() ,
,![]() ,垂足分别是
,垂足分别是![]() ,
,![]() ,
,![]() ,
,![]() ,直线
,直线![]() 交
交![]() 于点
于点![]() ,在
,在![]() 中,
中,![]() ,
,![]() ∴
∴![]() ∴
∴![]() ,我们称此公式
,我们称此公式![]() 为平面直角坐标系内任意两点
为平面直角坐标系内任意两点![]() ,
,![]() 间的距离公式
间的距离公式
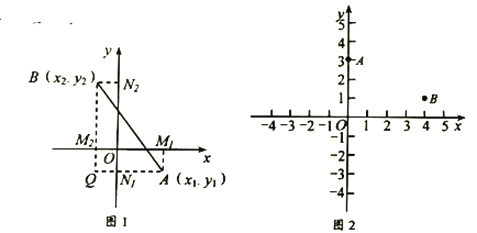
(1)直接应用平面内两点间距离公式计算点![]() ,
,![]() 的距离为_________
的距离为_________
(2)如图2,已知在平面直角坐标系中有两点![]() ,
,![]() ,
,![]() 为
为![]() 轴上任意一点,求
轴上任意一点,求![]() 的最小值
的最小值
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数![]() 图象的顶点坐标为(3,8),该二次函数图象的对称轴与x轴的交点为A,M是这个二次函数图象上的点,O是原点.
图象的顶点坐标为(3,8),该二次函数图象的对称轴与x轴的交点为A,M是这个二次函数图象上的点,O是原点.
(1)不等式b+2c+8≥0是否成立?请说明理由;
(2)设S是△AMO的面积,求满足S=9的所有点M的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列图形都是由相同的小正方形按照一定规律摆放而成,其中第1个图共有3个小正方形,第2个图共有8个小正方形,第3个图共有15个小正方形,第4个图共有24个小正方形,…,照此规律排列下去,则第8个图中小正方形的个数是( )
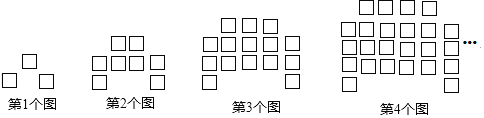
A. 48B. 63C. 80D. 99
查看答案和解析>>
科目:初中数学 来源: 题型:
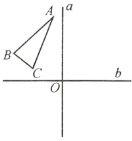
【题目】如图所示,已知![]() 和互相垂直的两条直线
和互相垂直的两条直线![]() 、
、![]() ,垂足为点
,垂足为点![]() .
.![]() 与
与![]() 关于直线
关于直线![]() 成轴对称,
成轴对称,![]() 与
与![]() 关于直线
关于直线![]() 成对称.那么下列说法正确的是( )
成对称.那么下列说法正确的是( )
A.![]() 可以由
可以由![]() 平移得到B.
平移得到B.![]() 可以由
可以由![]() 翻折得到
翻折得到
C.![]() 与
与![]() 成轴对称D.
成轴对称D.![]() 与
与![]() 成中心对称
成中心对称
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于a的方程2(a﹣2)=a+4的解也是关于x的方程2(x﹣3)﹣b=7的解.
(1)求a、b的值;
(2)若线段AB=a,在直线AB上取一点P,恰好使![]() =b,点Q为PB的中点,请画出图形并求出线段AQ的长.
=b,点Q为PB的中点,请画出图形并求出线段AQ的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com