
【题目】用棋子摆成的“上”字型图案如图所示现察此图案的规律,并回答:
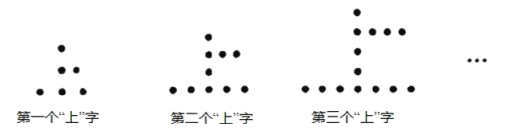
(1)依照此规律,第五个图形中共有 个棋子,第八个图形中共有 个棋子.
(2)第![]() (
(![]() 为正整数)个图形中共有 个棋子.
为正整数)个图形中共有 个棋子.
(3)根据(2)中的结论,第几个图形中有2022个棋子?
【答案】(1)22,34;(2)![]() ;(3)第505个图形中有2022个棋子
;(3)第505个图形中有2022个棋子
【解析】
(1)根据图形可以写出前几个图形中棋子的个数,从而发现棋子的变化规律,从而可以得到第五个和第八个图形中的棋子个数;
(2)根据(1)中发现的规律,可以得到第n(n为正整数)个图形中棋子的个数;
(3)根据(2)中的结果,可以求得第几个图形中有2022个棋子.
(1)由图可得:
第一图形中的“上”字中棋子的个数为:3×2=6,
第二图形中的“上”字中棋子的个数为:5×2=10,
第三图形中的“上”字中棋子的个数为:7×2=14,
…,
则第五个图形中共有:(2×5+1)×2=22(个),
第八个图形中共有:(2×8+1)×2=34(个).
故答案为:22,34;
(2)第n(n为正整数)个图形中共有:(2n+1)×2=(4n+2)(个).
故答案为:(4n+2);
(3)令4n+2=2022,
解得:n=505,
即第505个图形中有2022个棋子.


 夺冠训练单元期末冲刺100分系列答案
夺冠训练单元期末冲刺100分系列答案 新思维小冠军100分作业本系列答案
新思维小冠军100分作业本系列答案 名师指导一卷通系列答案
名师指导一卷通系列答案科目:初中数学 来源: 题型:
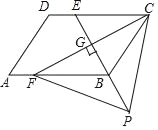
【题目】如图,四边形ABCD是平行四边形,点E是边CD上的一点,且BC=EC,CF⊥BE交AB于点F,P是EB延长线上一点,下列结论:①BE平分∠CBF;②CF平分∠DCB;③BC=FB;④PF=PC.其中正确的有_____.(填序号)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一只箱子里共有3个球,其中2个白球,1个红球,它们除颜色外均相同。
(1)从箱子中任意摸出一个球是白球的概率是多少?
(2)从箱子中任意摸出一个球,不将它放回箱子,搅匀后再摸出一个球,求两次摸出球的都是白球的概率,并画出树状图。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:正方形ABCD,等腰直角三角板的直角顶点落在正方形的顶点D处,使三角板绕点D旋转.
(1)当三角板旋转到图1的位置时,猜想CE与AF的数量关系,并加以证明;
(2)在(1)的条件下,若DE:AE:CE= 1: ![]() :3,求∠AED的度数;
:3,求∠AED的度数;
(3)若BC= 4,点M是边AB的中点,连结DM,DM与AC交于点O,当三角板的一边DF与边DM重合时(如图2),若OF=![]() ,求CN的长.
,求CN的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
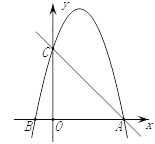
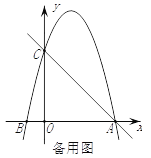
【题目】如图,在平面直角坐标系中,已知点C(0,4),点A、B在x轴上,并且OA=OC=4OB,动点P在过A、B、C三点的抛物线上.
(1)求抛物线的函数表达式;
(2)在直线AC上方的抛物线上,是否存在点P,使得△PAC的面积最大?若存在,求出P点坐标及ΔPAC面积的最大值;若不存在,请说明理由.
(3)在x轴上是否存在点Q,使得△ACQ是等腰三角形?若存在,请直接写出点Q的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若将代数式中的任意两个字母交换,代数式不变,则称这个代数式为完全对称式,如a+b+c就是完全对称式.下列三个代数式:①(a﹣b)2;②ab+bc+ca;③a2b+b2c+c2a.其中是完全对称式的是( )
A. ①②③ B. ①③ C. ②③ D. ①②
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在菱形ABCD中MN分别在AB、CD上且AM=CN,MN与AC交于点O,连接BO若∠DAC=62°,则∠OBC的度数为( )
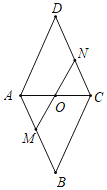
A. 28°B. 52°C. 62°D. 72°
查看答案和解析>>
科目:初中数学 来源: 题型:
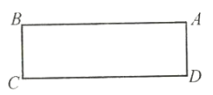
【题目】如图,在长方形![]() 中,
中,![]() ,
,![]() ,将长方形
,将长方形![]() 绕点
绕点![]() 逆时针旋转
逆时针旋转![]() ,点
,点![]() 、
、![]() 、
、![]() 分别对应点
分别对应点![]() 、
、![]() 、
、![]() .
.
(1)画出长方形![]() ;
;
(2)联结![]() 、
、![]() 、
、![]() ,请用含有
,请用含有![]() 、
、![]() 的代数式表示
的代数式表示![]() 的面积;
的面积;
(3)如果![]() 交
交![]() 于点
于点![]() ,请用含有
,请用含有![]() 、
、![]() 的代数式表示
的代数式表示![]() 的长度.
的长度.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com