
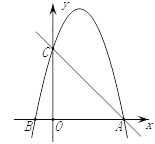
【题目】如图,在平面直角坐标系中,已知点C(0,4),点A、B在x轴上,并且OA=OC=4OB,动点P在过A、B、C三点的抛物线上.
(1)求抛物线的函数表达式;
(2)在直线AC上方的抛物线上,是否存在点P,使得△PAC的面积最大?若存在,求出P点坐标及ΔPAC面积的最大值;若不存在,请说明理由.
(3)在x轴上是否存在点Q,使得△ACQ是等腰三角形?若存在,请直接写出点Q的坐标;若不存在,请说明理由.
【答案】(1)y=x2+3x+4;(2)存在, 当P点坐标为(2,6)时,ΔPAC面积的最大值是8;(3)Q(0,0),(-4,0),![]() .
.
【解析】试题分析:(1)根据点C的坐标,即可求得OC的长,再求得点A、B的坐标,利用待定系数法即可求得函数的解析式;(2)存在,作PN⊥x轴交AC于N,先求得直线AC的解析式,设P(x,x2+3x+4),则N(x,-x+4),即可得PN=x2+4x ,根据三角形的面积公式可得S△PAC=![]() PN×4=-2(x-2)2+8 ,根据二次函数的性质可得当x=2时,ΔPAC面积的最大值为8,再求得点P的坐标即可;(3)根据勾股定理求得AC=4
PN×4=-2(x-2)2+8 ,根据二次函数的性质可得当x=2时,ΔPAC面积的最大值为8,再求得点P的坐标即可;(3)根据勾股定理求得AC=4![]() ,以A为顶点,以AC为腰时,可得AQ=4
,以A为顶点,以AC为腰时,可得AQ=4![]() ,此时可得Q的坐标为(4+4
,此时可得Q的坐标为(4+4![]() ,0)、(4-4
,0)、(4-4![]() ,0);以C为顶点,以AC为腰时,AC=AQ,因OC垂直于x轴,可得OA=OQ,此时点Q的坐标为(-4,0);以O为顶点,以AC为底边时,此时点Q的坐标为(0,0),所以符合条件的点Q的坐标为:(0,0),(-4,0),
,0);以C为顶点,以AC为腰时,AC=AQ,因OC垂直于x轴,可得OA=OQ,此时点Q的坐标为(-4,0);以O为顶点,以AC为底边时,此时点Q的坐标为(0,0),所以符合条件的点Q的坐标为:(0,0),(-4,0),![]() .
.
试题解析:
(1)∵C(0,4),∴OC=4.
∵OA=OC=4OB,∴OA=4,OB=1,
∴A(4,0),B(1,0),
设抛物线解析式:y=a(x+1)(x4),
∴4=4a,∴a=1.
∴y=x2+3x+4.
(2)存在.
作PN⊥x轴交AC于N,求得AC的解析式为y=-x+4 ,

设P(x,x2+3x+4),则N(x,-x+4),
得PN=(x2+3x+4)-(-x+4)=x2+4x ,
∴S△PAC=![]() PN×4=2PN=2(x2+4x)=-2(x-2)2+8 ,
PN×4=2PN=2(x2+4x)=-2(x-2)2+8 ,
当x=2时,ΔPAC面积的最大值为8,此时点P的坐标为(2,6).
∴P点坐标为(2,6)时,ΔPAC面积有最大值,最大面积是8 .
(3) 根据勾股定理求得AC=4![]() ,分三种情况:
,分三种情况:
①以A为顶点,以AC为腰时,可得AQ=4![]() ,此时可得Q的坐标为(4+4
,此时可得Q的坐标为(4+4![]() ,0)、(4-4
,0)、(4-4![]() ,0);
,0);
②以C为顶点,以AC为腰时,AC=AQ,因OC垂直于x轴,可得OA=OQ,此时点Q的坐标为(-4,0);
③以O为顶点,以AC为底边时,此时点Q的坐标为(0,0),
综上,符合条件的点Q的坐标为:(0,0),(-4,0),![]() .
.


科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,A、B为x轴上两点,C、D为y轴上的两点,经过点A、C、B的抛物线的一部分c1与经过点A、D、B的抛物线的一部分c2组合成一条封闭曲线,我们把这条封闭曲线成为“蛋线”.已知点C的坐标为(0,﹣![]() ),点M是抛物线C2:y=mx2﹣2mx﹣3m(m<0)的顶点.
),点M是抛物线C2:y=mx2﹣2mx﹣3m(m<0)的顶点.
(1)求A、B两点的坐标;
(2)“蛋线”在第四象限上是否存在一点P,使得△PBC的面积最大?若存在,求出△PBC面积的最大值;若不存在,请说明理由;
(3)当△BDM为直角三角形时,求m的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有20筐白菜,以每筐30千克为标准,超过或不足的分别用正、负来表示,记录如下:
与标准质量的差(单位:千克) | -3 | -2 | -1.5 | 0 | 1 | 2.5 |
筐数 | 1 | 4 | 2 | 3 | 2 | 8 |
(1)20筐白菜中,最重的一筐比最轻的一筐要重多少千克?
(2)与标准质量比较,20筐白菜总计超过或不足多少千克?
(3)若白菜每千克售价2元,则出售这20筐白菜可卖多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD的对角线相交于点O,DE∥AC,CE∥BD.
(1)求证:四边形OCED是菱形;
(2)若∠CAB=60,BC的长为![]() ,求四边形OCED的周长
,求四边形OCED的周长

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们知道:点A、B在数轴上分别表示有理数a、b,A、B两点之间的距离表示为AB,在数轴上A、B两点之间的距离AB=|a﹣b|.所以式子|x﹣3|的几何意义是数轴上表示有理数3的点与表示有理数x的点之间的距离.
根据上述材料,直接下列问题答案:
(1)|5﹣(﹣2)|的值为_____;
(2)若|x﹣3|=1,则x的值为_____;
(3)若|x﹣3|=|x+1|,则x的值为_____;
(4)若|x﹣3|+|x+1|=7,则x的值为_____.
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】用棋子摆成的“上”字型图案如图所示现察此图案的规律,并回答:
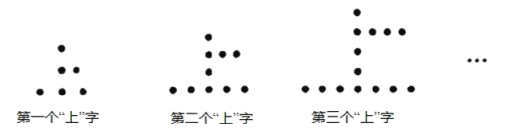
(1)依照此规律,第五个图形中共有 个棋子,第八个图形中共有 个棋子.
(2)第![]() (
(![]() 为正整数)个图形中共有 个棋子.
为正整数)个图形中共有 个棋子.
(3)根据(2)中的结论,第几个图形中有2022个棋子?
查看答案和解析>>
科目:初中数学 来源: 题型:
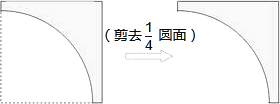
【题目】现在把一张正方形纸片按如图方式剪去一个半径为40![]() 厘米的圆面后得到如图纸片,且该纸片所能剪出的最大圆形纸片刚好能与前面所剪的扇形纸片围成一圆锥表面,则该正方形纸片的边长约为( )厘米.(不计损耗、重叠,结果精确到1厘米,
厘米的圆面后得到如图纸片,且该纸片所能剪出的最大圆形纸片刚好能与前面所剪的扇形纸片围成一圆锥表面,则该正方形纸片的边长约为( )厘米.(不计损耗、重叠,结果精确到1厘米,![]() ≈1.41,
≈1.41,![]() ≈1.73)
≈1.73)
A. 64 B. 67 C. 70 D. 73
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知一元二次方程ax2+bx+c=0(a≠0)中,下列说法:
①若a+b+c=0,则b2﹣4ac>0;
②若方程两根为﹣1和2,则2a+c=0;
③若方程ax2+c=0有两个不相等的实根,则方程ax2+bx+c=0必有两个不相等的实根;
④若b=2a+c,则方程有两个不相等的实根.其中正确的有( )
A. ①②③ B. ①②④ C. ②③④ D. ①②③④
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com