
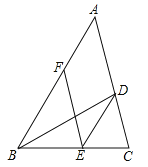
【题目】如图,BD是△ABC的角平分线,点E,F分别在BC,AB上,且DE∥AB,BE=AF.
(1)求证:四边形ADEF是平行四边形;
(2)若∠ABC=60°,BD=4,求平行四边形ADEF的面积.
【答案】(1)答案见解析;(2)![]() .
.
【解析】试题分析:(1)已知BD是△ABC的角平分线,根据角平分线的定义可得∠ABD=∠DBE;再由DE∥AB,根据两直线平行,内错角相等可得∠ABD=∠BDE,所有∠DBE=∠BDE,根据等腰三角形的性质可得BE=DE;再由BE=AF,可得AF=DE;根据一组对边平行且相等的四边形即可判定四边形ADEF是平行四边形;(2)过点D作DG⊥AB于点G,过点E作EH⊥BD于点H,易求得DG与DE的长,继而求得答案.
试题解析:
(1)证明:∵BD是△ABC的角平分线,
∴∠ABD=∠DBE,
∵DE∥AB,
∴∠ABD=∠BDE,
∴∠DBE=∠BDE,
∴BE=DE;
∵BE=AF,
∴AF=DE;
∴四边形ADEF是平行四边形;
(2)过点D作DG⊥AB于点G,过点E作EH⊥BD于点H,
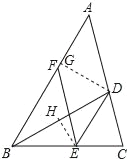
∵∠ABC=60°,BD是∠ABC的平分线,
∴∠ABD=∠EBD=30°,
∴DG=![]() BD=
BD=![]() ×4=2,
×4=2,
∵BE=DE,
∴BH=DH=2,
∴BE=![]() =
=![]() ,
,
∴DE=![]() ,
,
∴四边形ADEF的面积为:DEDG=![]() .
.


 100分闯关期末冲刺系列答案
100分闯关期末冲刺系列答案 名校联盟快乐课堂系列答案
名校联盟快乐课堂系列答案科目:初中数学 来源: 题型:
【题目】阅读下列材料,完成(1)、(2)小题.在平面直角坐标系中,已知![]() 轴上两点
轴上两点![]() ,
,![]() 的距离记作
的距离记作![]() ,如果
,如果![]() ,
,![]() 是平面上任意两点,我们可以通过构造直角三角形来求
是平面上任意两点,我们可以通过构造直角三角形来求![]() 间的距离,如图1,过点
间的距离,如图1,过点![]() 、
、![]() 分别向
分别向![]() 轴、
轴、![]() 轴作垂线
轴作垂线![]() ,
,![]() 和
和![]() ,
,![]() ,垂足分别是
,垂足分别是![]() ,
,![]() ,
,![]() ,
,![]() ,直线
,直线![]() 交
交![]() 于点
于点![]() ,在
,在![]() 中,
中,![]() ,
,![]() ∴
∴![]() ∴
∴![]() ,我们称此公式
,我们称此公式![]() 为平面直角坐标系内任意两点
为平面直角坐标系内任意两点![]() ,
,![]() 间的距离公式
间的距离公式
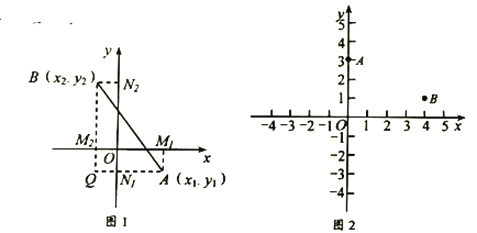
(1)直接应用平面内两点间距离公式计算点![]() ,
,![]() 的距离为_________
的距离为_________
(2)如图2,已知在平面直角坐标系中有两点![]() ,
,![]() ,
,![]() 为
为![]() 轴上任意一点,求
轴上任意一点,求![]() 的最小值
的最小值
查看答案和解析>>
科目:初中数学 来源: 题型:
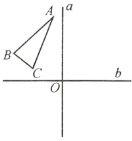
【题目】如图所示,已知![]() 和互相垂直的两条直线
和互相垂直的两条直线![]() 、
、![]() ,垂足为点
,垂足为点![]() .
.![]() 与
与![]() 关于直线
关于直线![]() 成轴对称,
成轴对称,![]() 与
与![]() 关于直线
关于直线![]() 成对称.那么下列说法正确的是( )
成对称.那么下列说法正确的是( )
A.![]() 可以由
可以由![]() 平移得到B.
平移得到B.![]() 可以由
可以由![]() 翻折得到
翻折得到
C.![]() 与
与![]() 成轴对称D.
成轴对称D.![]() 与
与![]() 成中心对称
成中心对称
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】江南新校区建设需运送3×105立方米的土石方,闽北运输公司承担了该项工程的运送任务.
(1)写出完成运送任务所需的时间y(单位:天)与公司平均每天的运送量x(单位:立方米/天)之间的关系式是 ;
(2)如果公司平均每天的运送量比原计划提高20%,按这个进度公司可以比规定时间提前10天完成运送任务,那么公司平均每天的运送量x是多少?
(3)实际运送时,公司派出80辆车,每辆车按问题(2)中提高后的运送量运输,若先运送了25天,后来由于工程进度的需要,剩下的任务须在20天内完成,那么公司至少要增加多少辆同样型号的车才能按时完成任务?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校开展以“迎新年”为主题的艺术活动,举办了四个项目的比赛.它们分别是:A演讲、B唱歌、C书法、D绘画.要求每位同学必须参加且限报一项.以九(一)班为样本进行统计,并将统计结果绘制如下两幅统计图,请你结合图中所给出的信息解答下列问题:
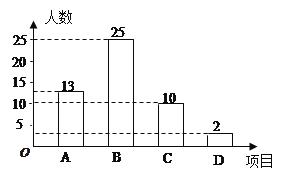
(1)求出参加绘画比赛的学生人数占全班总人数的百分比;
(2)求出扇形统计图中参加书法比赛的学生所在的扇形圆心角的度数;

(3)若该校九年级学生共有500人,请你估计这次活动中参加演讲和唱歌的学生共有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某体育用品商场预测某品牌运动服能够畅销,就用32000元购进了一批这种运动服,上市后很快脱销,商场又用68000元购进第二批这种运动服,所购数量是第一批购进数量的2倍,但每套进价多了10元.
(1)该商场两次共购进这种运动服多少套?
(2)如果这两批运动服每套的售价相同,且全部售完后总利润不低于20%,那么每套售价至少是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于a的方程2(a﹣2)=a+4的解也是关于x的方程2(x﹣3)﹣b=7的解.
(1)求a、b的值;
(2)若线段AB=a,在直线AB上取一点P,恰好使![]() =b,点Q为PB的中点,请画出图形并求出线段AQ的长.
=b,点Q为PB的中点,请画出图形并求出线段AQ的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】观察下列两个等式:![]() ,
,![]() ,给出定义如下:我们称使等式a﹣b=ab+1的成立的一对有理数a,b为“共生有理数对”,记为(a,b),如:数对
,给出定义如下:我们称使等式a﹣b=ab+1的成立的一对有理数a,b为“共生有理数对”,记为(a,b),如:数对![]() ,
,![]() ,都是“共生有理数对”.
,都是“共生有理数对”.
(1)数对![]() ,
,![]() 中是“共生有理数对”的是 ;
中是“共生有理数对”的是 ;
(2)若(m,n)是“共生有理数对”,则(﹣n,﹣m) “共生有理数对”(填“是”或“不是”);
(3)请再写出一对符合条件的“共生有理数对”为 ;(注意:不能与题目中已有的“共生有理数对”重复)
(4)若(a,3)是“共生有理数对”,求a的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,⊙O的直径AB=12,P是弦BC上一动点(与点B,C不重合),∠ABC=30°,过点P作PD⊥OP交⊙O于点D.
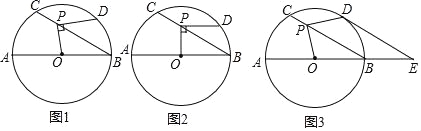
(1)如图2,当PD∥AB时,求PD的长;
(2)如图3,当![]() 时,延长AB至点E,使BE=
时,延长AB至点E,使BE=![]() AB,连接DE.
AB,连接DE.
①求证:DE是⊙O的切线;
②求PC的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com