
【题目】江南新校区建设需运送3×105立方米的土石方,闽北运输公司承担了该项工程的运送任务.
(1)写出完成运送任务所需的时间y(单位:天)与公司平均每天的运送量x(单位:立方米/天)之间的关系式是 ;
(2)如果公司平均每天的运送量比原计划提高20%,按这个进度公司可以比规定时间提前10天完成运送任务,那么公司平均每天的运送量x是多少?
(3)实际运送时,公司派出80辆车,每辆车按问题(2)中提高后的运送量运输,若先运送了25天,后来由于工程进度的需要,剩下的任务须在20天内完成,那么公司至少要增加多少辆同样型号的车才能按时完成任务?
【答案】(1)y=![]() ;(2)公司平均每天的运送量是5000立方米;(3)那么公司至少要增加20辆同样型号的车才能按时完成任务.
;(2)公司平均每天的运送量是5000立方米;(3)那么公司至少要增加20辆同样型号的车才能按时完成任务.
【解析】分析:(1)根据时间=![]() 列式,是反比例关系;
列式,是反比例关系;
(2)根据时间差为10天列分式方程,解出即可,要检验;
(3)根据题意列式计算即可.要先分别计算出平均每天每辆汽车运送土石方,80辆卡车工作25天运送的土石方,剩余的土石方在20天内全部运送完成需卡车,再计算公司要按时完成任务需增加卡车数量.
详解:(1)完成运送任务所需的时间y(单位:天)与公司平均每天的运送量x(单位:立方米/天)之间的关系式为:y=![]() .
.
故答案为:y=![]() .
.
(2)根据题意得:![]() ﹣
﹣![]() =10,
=10,
解方程得:x=5000,
经检验:x=5000是原方程的解,
答:公司平均每天的运送量是5000立方米;
(3)平均每天每辆车运送土石方(1.2×5000)÷80=75(m3),
80辆卡车工作25天运送的土石方为25×6000=150000(m3),
剩余的土石方在20天内全部运送完成需车(3×105﹣150000)÷(75×20)=100(辆),
所以公司要按时完成任务需至少再增加同样型号的车100﹣80=20(辆).
答:那么公司至少要增加20辆同样型号的车才能按时完成任务.


科目:初中数学 来源: 题型:
【题目】若将代数式中的任意两个字母交换,代数式不变,则称这个代数式为完全对称式,如a+b+c就是完全对称式.下列三个代数式:①(a﹣b)2;②ab+bc+ca;③a2b+b2c+c2a.其中是完全对称式的是( )
A. ①②③ B. ①③ C. ②③ D. ①②
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某电视台的一档娱乐性节目中,在游戏PK环节,为了随机分选游戏双方的组员,主持人设计了以下游戏:用不透明的白布包住三根颜色长短相同的细绳AA1、BB1、CC1,只露出它们的头和尾(如图所示),由甲、乙两位嘉宾分别从白布两端各选一根细绳,并拉出,若两人选中同一根细绳,则两人同队,否则互为反方队员.
(1)若甲嘉宾从中任意选择一根细绳拉出,求他恰好抽出细绳AA1的概率;
(2)请用画树状图法或列表法,求甲、乙两位嘉宾能分为同队的概率.
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
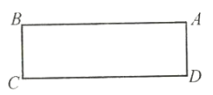
【题目】如图,在长方形![]() 中,
中,![]() ,
,![]() ,将长方形
,将长方形![]() 绕点
绕点![]() 逆时针旋转
逆时针旋转![]() ,点
,点![]() 、
、![]() 、
、![]() 分别对应点
分别对应点![]() 、
、![]() 、
、![]() .
.
(1)画出长方形![]() ;
;
(2)联结![]() 、
、![]() 、
、![]() ,请用含有
,请用含有![]() 、
、![]() 的代数式表示
的代数式表示![]() 的面积;
的面积;
(3)如果![]() 交
交![]() 于点
于点![]() ,请用含有
,请用含有![]() 、
、![]() 的代数式表示
的代数式表示![]() 的长度.
的长度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:![]() 中,
中,![]() ,求证:
,求证:![]() ,下面写出可运用反证法证明这个命题的四个步骤:
,下面写出可运用反证法证明这个命题的四个步骤:
①∴![]() ,这与三角形内角和为
,这与三角形内角和为![]() 矛盾,②因此假设不成立.∴
矛盾,②因此假设不成立.∴![]() ,③假设在
,③假设在![]() 中,
中,![]() ,④由
,④由![]() ,得
,得![]() ,即
,即![]() .这四个步骤正确的顺序应是( )
.这四个步骤正确的顺序应是( )
A.③④②①B.③④①②C.①②③④D.④③①②
查看答案和解析>>
科目:初中数学 来源: 题型:
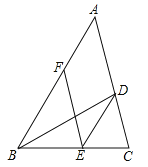
【题目】如图,BD是△ABC的角平分线,点E,F分别在BC,AB上,且DE∥AB,BE=AF.
(1)求证:四边形ADEF是平行四边形;
(2)若∠ABC=60°,BD=4,求平行四边形ADEF的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在数轴上,点A表示1,现将点A沿数轴做如下移动,第一次点A向左移动3个单位长度到达点A1,第二次将点A1向右移动6个单位长度到达点A2,第三次将点A2向左移动9个单位长度到达点A3,按照这种规律下去,第n次移动到点An,如果点An,与原点的距离不少于20,那么n的最小值是( )

A. 11B. 12C. 13D. 20
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,OC在∠BOD内.
(1)如果∠AOC和∠BOD都是直角.
①若∠BOC=60°,则∠AOD的度数是 ;
②猜想∠BOC与∠AOD的数量关系,并说明理由;
(2)如果∠AOC=∠BOD=x°,∠AOD=y°,求∠BOC的度数.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com