
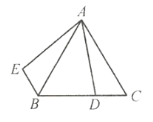
【题目】等边![]() 中,
中,![]() 在边
在边![]() 上,
上,![]() 绕顶点
绕顶点![]() 旋转到
旋转到![]() 位置,
位置,
(1)指出旋转中心,旋转方向,其中一个旋转角及其大小.
(2)指出![]() 的大小以及联结
的大小以及联结![]() 后
后![]() 的形状.
的形状.
科目:初中数学 来源: 题型:
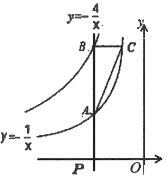
【题目】如图,点![]() 为
为![]() 轴负半轴上的一个点,过点
轴负半轴上的一个点,过点![]() 作
作![]() 轴的垂线,交函数
轴的垂线,交函数![]() 的图像于点
的图像于点![]() ,交函数
,交函数![]() 的图像于点
的图像于点![]() ,过点
,过点![]() 作
作![]() 轴的平行线,交
轴的平行线,交![]() 于点
于点![]() ,连接
,连接![]() .
.
(1)当点![]() 的坐标为(–1,0)时,求
的坐标为(–1,0)时,求![]() 的面积;
的面积;
(2)若![]() ,求点
,求点![]() 的坐标;
的坐标;
(3)连接![]() 和
和![]() .当点
.当点![]() 的坐标为(
的坐标为(![]() ,0)时,
,0)时,![]() 的面积是否随
的面积是否随![]() 的值的变化而变化?请说明理由.
的值的变化而变化?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数![]() 图象的顶点坐标为(3,8),该二次函数图象的对称轴与x轴的交点为A,M是这个二次函数图象上的点,O是原点.
图象的顶点坐标为(3,8),该二次函数图象的对称轴与x轴的交点为A,M是这个二次函数图象上的点,O是原点.
(1)不等式b+2c+8≥0是否成立?请说明理由;
(2)设S是△AMO的面积,求满足S=9的所有点M的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
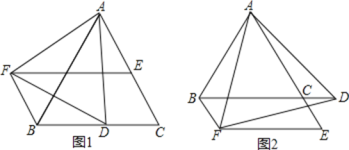
【题目】已知![]() 是等边三角形,D是BC边上的一个动点
是等边三角形,D是BC边上的一个动点![]() 点D不与B,C重合
点D不与B,C重合![]() 是以AD为边的等边三角形,过点F作BC的平行线交射线AC于点E,连接BF.
是以AD为边的等边三角形,过点F作BC的平行线交射线AC于点E,连接BF.
![]() 如图1,求证:
如图1,求证:![]() ≌
≌![]() ;
;
![]() 请判断图1中四边形BCEF的形状,并说明理由;
请判断图1中四边形BCEF的形状,并说明理由;
![]() 若D点在BC边的延长线上,如图2,其它条件不变,请问
若D点在BC边的延长线上,如图2,其它条件不变,请问![]() 中结论还成立吗?如果成立,请说明理由.
中结论还成立吗?如果成立,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
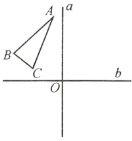
【题目】如图所示,已知![]() 和互相垂直的两条直线
和互相垂直的两条直线![]() 、
、![]() ,垂足为点
,垂足为点![]() .
.![]() 与
与![]() 关于直线
关于直线![]() 成轴对称,
成轴对称,![]() 与
与![]() 关于直线
关于直线![]() 成对称.那么下列说法正确的是( )
成对称.那么下列说法正确的是( )
A.![]() 可以由
可以由![]() 平移得到B.
平移得到B.![]() 可以由
可以由![]() 翻折得到
翻折得到
C.![]() 与
与![]() 成轴对称D.
成轴对称D.![]() 与
与![]() 成中心对称
成中心对称
查看答案和解析>>
科目:初中数学 来源: 题型:
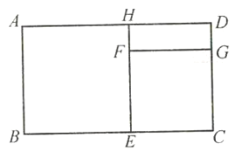
【题目】如图,长方形![]() 中,长
中,长![]() ,宽
,宽![]() ,四边形
,四边形![]() 和四边形
和四边形![]() 都是正方形.
都是正方形.
(1)求四边形![]() 的面积(用含
的面积(用含![]() 、
、![]() 的代数式表示);
的代数式表示);
(2)当![]() 、
、![]() 满足什么等量关系时,图形是一个轴对称图形.
满足什么等量关系时,图形是一个轴对称图形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】江南新校区建设需运送3×105立方米的土石方,闽北运输公司承担了该项工程的运送任务.
(1)写出完成运送任务所需的时间y(单位:天)与公司平均每天的运送量x(单位:立方米/天)之间的关系式是 ;
(2)如果公司平均每天的运送量比原计划提高20%,按这个进度公司可以比规定时间提前10天完成运送任务,那么公司平均每天的运送量x是多少?
(3)实际运送时,公司派出80辆车,每辆车按问题(2)中提高后的运送量运输,若先运送了25天,后来由于工程进度的需要,剩下的任务须在20天内完成,那么公司至少要增加多少辆同样型号的车才能按时完成任务?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某体育用品商场预测某品牌运动服能够畅销,就用32000元购进了一批这种运动服,上市后很快脱销,商场又用68000元购进第二批这种运动服,所购数量是第一批购进数量的2倍,但每套进价多了10元.
(1)该商场两次共购进这种运动服多少套?
(2)如果这两批运动服每套的售价相同,且全部售完后总利润不低于20%,那么每套售价至少是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】生活中,有人喜欢把传送的便条折成![]() 形状,折叠过程是这样的(阴影部分表示纸条的反面):如果由信纸折成的长方形纸条(图①)长为
形状,折叠过程是这样的(阴影部分表示纸条的反面):如果由信纸折成的长方形纸条(图①)长为![]() ,宽为
,宽为![]() ,分别回答下列问题:
,分别回答下列问题:
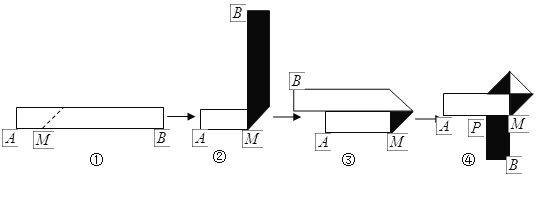
(1)为了保证能折成图④的形状(即纸条两端均超出点![]() ),试求
),试求![]() 的取值范围.
的取值范围.
(2)如果不但要折成图④的形状,而且为了美观,希望纸条两端超出点![]() 的长度相等,即最终图形是轴对称图形,试求在开始折叠时起点
的长度相等,即最终图形是轴对称图形,试求在开始折叠时起点![]() 与点
与点![]() 的距离(用
的距离(用![]() 表示)
表示)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com