
【题目】如图,点![]() 为
为![]() 轴负半轴上的一个点,过点
轴负半轴上的一个点,过点![]() 作
作![]() 轴的垂线,交函数
轴的垂线,交函数![]() 的图像于点
的图像于点![]() ,交函数
,交函数![]() 的图像于点
的图像于点![]() ,过点
,过点![]() 作
作![]() 轴的平行线,交
轴的平行线,交![]() 于点
于点![]() ,连接
,连接![]() .
.
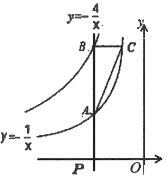
(1)当点![]() 的坐标为(–1,0)时,求
的坐标为(–1,0)时,求![]() 的面积;
的面积;
(2)若![]() ,求点
,求点![]() 的坐标;
的坐标;
(3)连接![]() 和
和![]() .当点
.当点![]() 的坐标为(
的坐标为(![]() ,0)时,
,0)时,![]() 的面积是否随
的面积是否随![]() 的值的变化而变化?请说明理由.
的值的变化而变化?请说明理由.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)
;(3)![]() 的面积不随t的值的变化而变化,理由见解析。
的面积不随t的值的变化而变化,理由见解析。
【解析】
(1)根据题意首先计算出C点的坐标,再计算三角形的面积.
(2)首先利用反比例函数的关系式设出A点的坐标,在表示B、C点的坐标,结合AB=BC求解未知数,即可的A点的坐标.
(3)过点C作![]() 轴于点E,
轴于点E,![]() 轴于点D,再根据P点的坐标表示A、B、C点的坐标,再利用
轴于点D,再根据P点的坐标表示A、B、C点的坐标,再利用![]() ,即可求解出
,即可求解出![]() 的面积.
的面积.
解:(1)当点P的坐标为![]() 时,点A、B的横坐标为-1,
时,点A、B的横坐标为-1,
∵点A在反比例函数![]() 上,点B在反比例函数
上,点B在反比例函数![]() 上,
上,
∴点![]() ,点
,点![]() .
.
![]() 轴,
轴,
∴点C的纵坐标为4,
又∵点C在![]() 上,∴点C的坐标为
上,∴点C的坐标为![]() ,
,
![]()
(2)设点A的坐标为![]() ,则
,则![]()
则![]()
得方程![]() ,解之,得
,解之,得![]() (含正),
(含正),
![]()
(3)过点C作![]() 轴于点E,
轴于点E,![]() 轴于点D。如图所示:
轴于点D。如图所示:
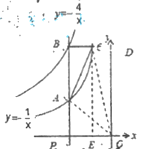
∵点P的坐标为![]() ,
,
∴点A的坐标为![]() ,点
,点![]() ,点
,点![]()
![]()
故![]() 的面积不随t的值的变化而变化
的面积不随t的值的变化而变化


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,以AB为直径作圆O,分别交BC于点D,交CA的延长线于点E,过点D作DH⊥AC于点H,连接DE交线段OA于点F.
(1)求证:DH是圆O的切线;
(2)若A为EH的中点,求![]() 的值;
的值;
(3)若EA=EF=1,求圆O的半径.

查看答案和解析>>
科目:初中数学 来源: 题型:
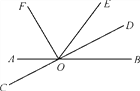
【题目】如图,直线AB与CD相交于点O,OF,OD分别是∠AOE,∠BOE的平分线.
(1)写出∠DOE的补角;
(2)若∠BOE=62°,求∠AOD和∠EOF的度数;
(3)试问射线OD与OF之间有什么特殊的位置关系?为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
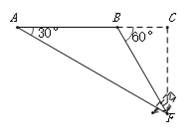
【题目】如图,在一次空中搜寻中,水平飞行的飞机观测到在点A俯角为30°方向的F点处有疑似飞机残骸的物体(该物体视为静止).为了便于观察,飞机继续向前飞行了800米到达B点,此时测得点F在点B俯角为60°的方向上,请你计算当飞机飞临F的正上方点C时(点A、B、C在同一直线上),竖直高度CF约为多少米?(结果保留整数,参考数值:![]() ≈1.7)
≈1.7)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:正方形ABCD,等腰直角三角板的直角顶点落在正方形的顶点D处,使三角板绕点D旋转.
(1)当三角板旋转到图1的位置时,猜想CE与AF的数量关系,并加以证明;
(2)在(1)的条件下,若DE:AE:CE= 1: ![]() :3,求∠AED的度数;
:3,求∠AED的度数;
(3)若BC= 4,点M是边AB的中点,连结DM,DM与AC交于点O,当三角板的一边DF与边DM重合时(如图2),若OF=![]() ,求CN的长.
,求CN的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若将代数式中的任意两个字母交换,代数式不变,则称这个代数式为完全对称式,如a+b+c就是完全对称式.下列三个代数式:①(a﹣b)2;②ab+bc+ca;③a2b+b2c+c2a.其中是完全对称式的是( )
A. ①②③ B. ①③ C. ②③ D. ①②
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了解本校九年级学生期末数学考试情况,小亮在九年级随机抽取了一部分学生的期末数学成绩为样本,分为A(100﹣90分)、B(89~80分)、C(79~60分)、D(59~0分)四个等级进行统计,并将统计结果绘制成如下统计图,请你根据统计图解答以下问题:
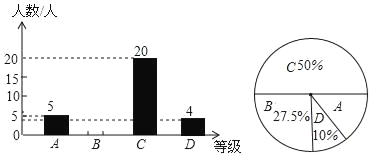
(1)这次随机抽取的学生共有多少人?
(2)请补全条形统计图;
(3)这个学校九年级共有学生1200人,若分数为80分(含80分)以上为优秀,请估计这次九年级学生期末数学考试成绩为优秀的学生人数大约有多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com