【题目】在
中，
，
是对角线
上不同的两点，下列条件中，不能得出四边形
一定为平行四边形的是（ ）
A. 
B. 
C. 
D. 
科目：初中数学 来源： 题型：
【题目】如表是一个4×4（4行4列共16个“数”组成）的奇妙方阵，从这个方阵中选四个“数”，而且这四个“数”中的任何两个不在同一行，也不在同一列，有很多选法，把每次选出的四个“数”相加，其和是定值，则方阵中第三行三列的“数”是（ ）
30 |
| 2 | 22 |
﹣3 | ﹣2 | ﹣ | 0 |
|﹣5| | 6 | 23 | |
（ | 4 |
| （ |
A. 5 B. 6 C. 7 D. 8
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】关于x的方程2（x﹣3）﹣m=2的解和方程3x﹣7=2x的解相同．
（1）求m的值；
（2）已知线段AB=m，在直线AB上取一点P，恰好使AP=2PB，点Q为PB的中点，求线段AQ的长．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】有这样一个问题:探究函数
的图象与性质.小东根据学习函数的经验，对函数的图象与性质进行了探究.
下面是小东的探究过程，请补充完整:
(1)函数的自变量x的取值范围是 ;
(2)下表是y与x的几组对应值.
x | … | -3 | -2 | -1 |
| 1 | 2 | 3 | 4 | 5 | … |
y | … |
|
|
|
| 3 |
|
|
| m | … |
求m的值;
(3)如下图，在平面直角坐标系xOy中，描出了以上表中各对对应值为坐标的点.根据描出的点，画出该函数的图象;
(4)结合函数的图象，写出该函数的一条性质: .
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，点
为
轴负半轴上的一个点，过点作轴的垂线，交函数
的图像于点
，交函数
的图像于点
，过点作轴的平行线，交于点
，连接
.
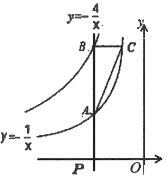
(1)当点的坐标为(–1，0)时，求
的面积;
(2)若
，求点的坐标;
(3)连接
和
.当点的坐标为(
，0)时，
的面积是否随的值的变化而变化?请说明理由.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，△ABC中，AB＝AC，以AB为直径的⊙O分别与BC、AC交于点D、E，过点D作⊙O的切线DF，交AC于点F．
（1）求证：DF⊥AC；
（2）若⊙O的半径为4，∠CDF＝22.5°，求阴影部分的面积．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】先阅读材料：如图（1），在数轴上
示的数为
，
点表示的数为
，则点到点的距离记为
.线段的长可以用右边的数减去左边的数表示，即
.
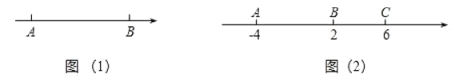
解决问题：如图（2），数轴上点表示的数是-4，点表示的数是2，点
表示的数是6.
（1）若数轴上有一点
，且
，则点表示的数为 ；
（2）点、、开始在数轴上运动，若点以每秒1个单位长度的速度向左运动，同时，若点和点分别以每秒2个单位长度和3个单位长度的速度向右运动，假设
秒钟过后，若点与点之间的距离表示为，点与点之间的距离表示为
，点与点之间的距离表示为
．则点表示的数是 （用含的代数式表示），
（用含的代数式表示）.
（3）请问：
的值是否随着时间的变化而改变？若变化，请说明理由；若不变，请求其值.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】下列四幅图象近似刻画两个变量之间的关系，请按图象顺序将下面四种情景与之对应排序（ ）.
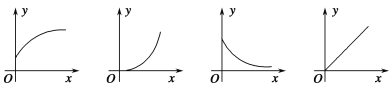
①一辆汽车在公路上匀速行驶（汽车行驶的路程与时间的关系）
②向锥形瓶中匀速注水（水面的高度与注水时间的关系）
③将常温下的温度计插入一杯热水中（温度计的读数与时间的关系）
④一杯越来越凉的水（水温与时间的关系）
A.①②④③ B.③④②①
C.①④②③ D.③②④①
查看答案和解析>>
科目：初中数学 来源： 题型：
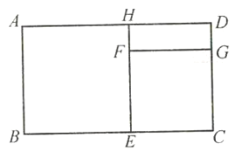
【题目】如图，长方形
中，长
，宽
，四边形
和四边形
都是正方形.
（1）求四边形
的面积（用含
、
的代数式表示）；
（2）当、满足什么等量关系时，图形是一个轴对称图形.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
