练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】生活中，有人喜欢把传送的便条折成形状，折叠过程是这样的（阴影部分表示纸条的反面）：如果由信纸折成的长方形纸条（图①）长为，宽为，分别回答下列问题：

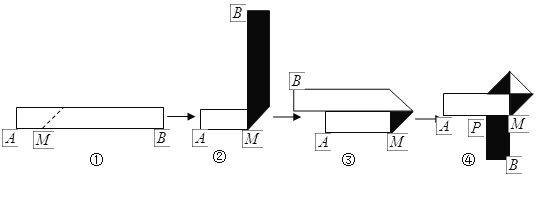
    （1）为了保证能折成图④的形状（即纸条两端均超出点），试求的取值范围．

    （2）如果不但要折成图④的形状，而且为了美观，希望纸条两端超出点的长度相等，即最终图形是轴对称图形，试求在开始折叠时起点与点的距离（用表示）

    【答案】(1) x＜5.2

    (2) 13－1.5x

    【解析】

    （1）按图中方式折叠后可得到除去两端，纸条使用的长度为5x，那么纸条使用的长度应大于0，小于纸条总长度．

    （2）是轴对称图形，那么AM=AP+x．

    解答：解：（1）由折纸过程可知0＜5x＜26，∴0＜x＜5.2．

    （2）∵图④为轴对称图形，∴AM=+x=13-1.5x，

    即点M与点A的距离是（13-1.5x）cm．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】等边中，在边上，绕顶点旋转到位置，

    （1）指出旋转中心，旋转方向，其中一个旋转角及其大小.

    （2）指出的大小以及联结后的形状.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在数轴上，点A表示1，现将点A沿数轴做如下移动，第一次点A向左移动3个单位长度到达点A1，第二次将点A1向右移动6个单位长度到达点A2，第三次将点A2向左移动9个单位长度到达点A3，按照这种规律下去，第n次移动到点An，如果点An，与原点的距离不少于20，那么n的最小值是（ ）

    A. 11B. 12C. 13D. 20

    查看答案和解析>>

    科目：初中数学 来源： 题型：

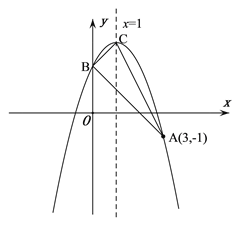
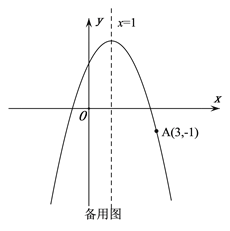
    【题目】如图，抛物线的顶点为C，对称轴为直线，且经过点A(3,－1)，与y轴交于点B.

    （1）求抛物线的解析式；

    （2）判断△ABC的形状，并说明理由；

    （3）经过点A的直线交抛物线于点P，交x轴于点Q，若，试求出点P的坐标.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

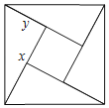
    【题目】如图，是用4个全等的直角三角形与1个小正方形镶嵌而成的正方形图案．已知大正方形面积为49，小正方形面积为4，若用，表示直角三角形的两直角边，下列四个说法：①；②；③；④；其中说法正确的是　　

    A. ①②B. ①②③C. ①②④D. ①②③④

    查看答案和解析>>

    科目：初中数学 来源： 题型：

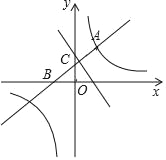
    【题目】如图，直线y=x+b与双曲线y=（k是常数，k≠0）在第一象限内交于点A（1，2），且与x轴、y轴分别交于B，C两点．点P在x轴．

    （1）求直线和双曲线的解析式；

    （2）若△BCP的面积等于2，求P点的坐标；

    （3）求PA+PC的最短距离．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，OC在∠BOD内．

    （1）如果∠AOC和∠BOD都是直角．

    ①若∠BOC=60°，则∠AOD的度数是　 　；

    ②猜想∠BOC与∠AOD的数量关系，并说明理由；

    （2）如果∠AOC=∠BOD=x°，∠AOD=y°，求∠BOC的度数．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

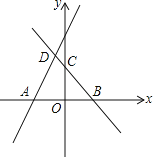
    【题目】如图，直线y=x+m与x轴交于点A（-3，0），直线y=-x+2与x轴、y轴分别交于B、C两点，并与直线y=x+m相交于点D，

    （1）点D的坐标为 ；

    （2）求四边形AOCD的面积；

    （3）若点P为x轴上一动点，当PD+PC的值最小时，求点P的坐标．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】计算：

    （1）﹣28﹣（﹣15）+（﹣17）﹣（+5）

    （2）（﹣72）×2

    （3）

    （4）

    （5）3m2﹣mn﹣2m2+4mn

    （6）（3x2﹣xy﹣2y2）﹣2（x2+xy﹣2y2）

    查看答案和解析>>

    同步练习册答案