【题目】如图，在数轴上，点A表示1，现将点A沿数轴做如下移动，第一次点A向左移动3个单位长度到达点A1，第二次将点A1向右移动6个单位长度到达点A2，第三次将点A2向左移动9个单位长度到达点A3，按照这种规律下去，第n次移动到点An，如果点An，与原点的距离不少于20，那么n的最小值是（ ）
A. 11B. 12C. 13D. 20
【答案】C
【解析】
当n为奇数的点在点A的左边，各点所表示的数依次减少3，当n为偶数的点在点A的右侧，各点所表示的数依次增加3．
根据题目已知条件，A1表示的数，1﹣3=﹣2；A2表示的数为﹣2+6=4；A3表示的数为4﹣9=﹣5；A4表示的数为﹣5+12=7；A5表示的数为7﹣15=﹣8；A6表示的数为7+3=10，A7表示的数为﹣8﹣3=﹣11，A8表示的数为10+3=13，A9表示的数为﹣11﹣3=﹣14，A10表示的数为13+3=16，A11表示的数为﹣14﹣3=﹣17，A12表示的数为16+3=19，A13表示的数为﹣17﹣3=﹣20．
所以点An与原点的距离不小于20，那么n的最小值是13．
故选C．
科目：初中数学 来源： 题型：
【题目】已知二次函数
图象的顶点坐标为（3，8），该二次函数图象的对称轴与x轴的交点为A，M是这个二次函数图象上的点，O是原点．
（1）不等式b+2c+8≥0是否成立？请说明理由；
（2）设S是△AMO的面积，求满足S=9的所有点M的坐标．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】江南新校区建设需运送3×105立方米的土石方，闽北运输公司承担了该项工程的运送任务．
（1）写出完成运送任务所需的时间y（单位：天）与公司平均每天的运送量x（单位：立方米/天）之间的关系式是 ；
（2）如果公司平均每天的运送量比原计划提高20%，按这个进度公司可以比规定时间提前10天完成运送任务，那么公司平均每天的运送量x是多少？
（3）实际运送时，公司派出80辆车，每辆车按问题（2）中提高后的运送量运输，若先运送了25天，后来由于工程进度的需要，剩下的任务须在20天内完成，那么公司至少要增加多少辆同样型号的车才能按时完成任务？
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】某体育用品商场预测某品牌运动服能够畅销，就用32000元购进了一批这种运动服，上市后很快脱销，商场又用68000元购进第二批这种运动服，所购数量是第一批购进数量的2倍，但每套进价多了10元．
（1）该商场两次共购进这种运动服多少套？
（2）如果这两批运动服每套的售价相同，且全部售完后总利润不低于20%，那么每套售价至少是多少元？
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】已知关于a的方程2（a﹣2）＝a+4的解也是关于x的方程2（x﹣3）﹣b＝7的解．
（1）求a、b的值；
（2）若线段AB＝a，在直线AB上取一点P，恰好使
＝b，点Q为PB的中点，请画出图形并求出线段AQ的长．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】现有一个种植总面积为
的矩形塑料温棚，分垄间隔套种草莓和西红柿共
垄，种植的草莓或西红柿单种农作物的总垄数不低于8垄，又不超过
垄(垄数为正整数)，它们的占地面积、产量、利润分别如下：
⑴若设草莓共种植了
垄，通过计算说明共有几种种植方案？分别是哪几种？
⑵在这几种种植方案中，哪种方案获得的利润最大？最大利润是多少？
占地面积（m2/垄） | 产量（千克/垄） | 利润（元/千克） | |
西红柿 | 32 | 160 | 1.0 |
草莓 | 15 | 50 | 1.6 |
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】观察下列两个等式：
，
，给出定义如下：我们称使等式a﹣b＝ab+1的成立的一对有理数a，b为“共生有理数对”，记为（a，b），如：数对
，
，都是“共生有理数对”．
（1）数对
，
中是“共生有理数对”的是 ；
（2）若（m，n）是“共生有理数对”，则（﹣n，﹣m） “共生有理数对”（填“是”或“不是”）；
（3）请再写出一对符合条件的“共生有理数对”为 ；（注意：不能与题目中已有的“共生有理数对”重复）
（4）若（a，3）是“共生有理数对”，求a的值．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】生活中，有人喜欢把传送的便条折成
形状，折叠过程是这样的（阴影部分表示纸条的反面）：如果由信纸折成的长方形纸条（图①）长为
，宽为
，分别回答下列问题：
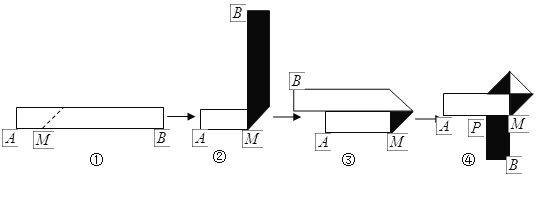
（1）为了保证能折成图④的形状（即纸条两端均超出点
），试求的取值范围．
（2）如果不但要折成图④的形状，而且为了美观，希望纸条两端超出点的长度相等，即最终图形是轴对称图形，试求在开始折叠时起点
与点的距离（用表示）
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】O为直线AB上的一点，OC⊥OD，射线OE平分∠AOD.
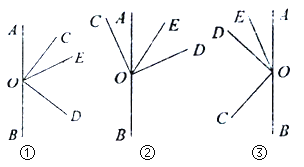
(1)如图①，判断∠COE和∠BOD之间的数量关系，并说明理由；
(2)若将∠COD绕点O旋转至图②的位置，试问(1)中∠COE和∠BOD之间的数量关系是否发生变化？并说明理由；
(3)若将∠COD绕点O旋转至图③的位置，探究∠COE和∠BOD之间的数量关系，并说明理由．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com