
°æƒø°øœ÷”–“ª∏ˆ÷÷÷≤◊Ð√ʪ˝Œ™![]() µƒæÿ–ŒÀСœŒ¬≈Ô£¨∑÷¬¢º‰∏ÙÃ◊÷÷≤ððÆ∫ÕŒ˜∫Ï ¡π≤
µƒæÿ–ŒÀСœŒ¬≈Ô£¨∑÷¬¢º‰∏ÙÃ◊÷÷≤ððÆ∫ÕŒ˜∫Ï ¡π≤![]() ¬¢£¨÷÷÷≤µƒ≤ððƪڌ˜∫Ï ¡µ•÷÷≈©◊˜ŒÔµƒ◊Ь¢ ˝≤ªµÕ”⁄8¬¢£¨”÷≤ª≥¨π˝
¬¢£¨÷÷÷≤µƒ≤ððƪڌ˜∫Ï ¡µ•÷÷≈©◊˜ŒÔµƒ◊Ь¢ ˝≤ªµÕ”⁄8¬¢£¨”÷≤ª≥¨π˝![]() ¬¢(¬¢ ˝Œ™’˝’˚ ˝)£¨À¸√«µƒ’ºµÿ√ʪ˝°¢≤˙¡ø°¢¿˚»Û∑÷±»Áœ¬£∫
¬¢(¬¢ ˝Œ™’˝’˚ ˝)£¨À¸√«µƒ’ºµÿ√ʪ˝°¢≤˙¡ø°¢¿˚»Û∑÷±»Áœ¬£∫
¢≈»Ù…Ë≤ððÆπ≤÷÷÷≤¡À![]() ¬¢£¨Õ®π˝º∆À„Àµ√˜π≤”–º∏÷÷÷÷÷≤∑Ω∞∏£ø∑÷± «ƒƒº∏÷÷£ø
¬¢£¨Õ®π˝º∆À„Àµ√˜π≤”–º∏÷÷÷÷÷≤∑Ω∞∏£ø∑÷± «ƒƒº∏÷÷£ø
¢∆‘⁄’‚º∏÷÷÷÷÷≤∑Ω∞∏÷–£¨ƒƒ÷÷∑Ω∞∏ªÒµ√µƒ¿˚»Û◊Ó¥Û£ø◊Ó¥Û¿˚»Û «∂ý…Ÿ£ø
’ºµÿ√ʪ˝£®m2/¬¢£© | ≤˙¡ø£®«ßøÀ/¬¢£© | ¿˚»Û£®‘™/«ßøÀ£© | |
Œ˜∫Ï ¡ | 32 | 160 | 1.0 |
≤ððÆ | 15 | 50 | 1.6 |
°æ¥∞∏°ø(1)π≤”–»˝÷÷÷÷÷≤∑Ω∞∏£¨æþÃÂ∑Ω∞∏º˚Ω‚Œˆ£ª(2)µ±≤ððÆ÷÷÷≤14¬¢£¨Œ˜∫Ï ¡÷÷÷≤10¬¢£¨ªÒµ√µƒ¿˚»Û◊Ó¥Û£¨◊Ó¥Û¿˚»Û «2720‘™.
°æΩ‚Œˆ°ø
(1)”…”⁄÷÷÷≤≤ððƪڌ˜∫Ï ¡¬¢ ˝ «≤ª»∑∂®µƒ£¨À˘“‘”¶¿˚”√≤ªµ» Ω¿¥Ω‚¥£Æ”…”⁄ÀСœŒ¬≈Ôµƒ÷÷÷≤√ʪ˝Œ™530m2£¨À˘“‘ø…“‘¡–≥ˆ≤ªµ» Ω15x+32(24-x)°Ð530£¨”…¥Àø…“‘œ»«Ûµ√xµƒ»°÷µ∑∂Œß£¨»ª∫Û‘Ÿ»∑∂®’˚ ˝xµƒ÷µ£¨¥”∂¯»∑∂®÷÷÷≤µƒ∑Ω∞∏£ª
(2)∏˘æð(2)÷–µƒ∑Ω∞∏∑÷±«Û≥ˆ√ø÷÷∑Ω∞∏ªÒµ√µƒ¿˚»ÛΩ¯––±»Ωœº¥ø…µ√.
(1)≤ððÆπ≤÷÷÷≤¡À![]() ¬¢£¨∏˘æð“‚Œ˜∫Ï ¡÷÷¡À(
¬¢£¨∏˘æð“‚Œ˜∫Ï ¡÷÷¡À(![]() )¬¢£¨‘Ú”–
)¬¢£¨‘Ú”–
15x+32(24-x)°Ð530£¨
Ω‚µ√x°ð14£¨
°þx°Ð16£¨«“x «’˝’˚ ˝£¨
°ýx=14£¨15£¨16
π≤”–»˝÷÷÷÷÷≤∑Ω∞∏£¨∑÷± «£∫
∑Ω∞∏“ª£∫≤ððÆ÷÷÷≤14¬¢£¨Œ˜∫Ï ¡÷÷÷≤10¬¢£ª
∑Ω∞∏∂˛£∫≤ððÆ÷÷÷≤15¬¢£¨Œ˜∫Ï ¡÷÷÷≤9¬¢£ª
∑Ω∞∏»˝£∫≤ððÆ÷÷÷≤16¬¢£¨Œ˜∫Ï ¡÷÷÷≤8¬¢£ª
(2)∑Ω∞∏“ªªÒµ√µƒ¿˚»Û£∫14°¡50°¡1.6+10°¡160°¡1.0=2720(‘™)£¨
∑Ω∞∏∂˛ªÒµ√µƒ¿˚»Û£∫15°¡50°¡1.6+9°¡160°¡1.0=2640(‘™)£¨
∑Ω∞∏»˝ªÒµ√µƒ¿˚»Û£∫16°¡50°¡1.6+8°¡160°¡1.0=2560(‘™)£¨
À˘“‘µ±≤ððÆ÷÷÷≤14¬¢£¨Œ˜∫Ï ¡÷÷÷≤10¬¢£¨ªÒµ√µƒ¿˚»Û◊Ó¥Û£¨◊Ó¥Û¿˚»Û «2720‘™.


 ‘ƒ∂¡øÏ≥µœµ¡–¥∞∏
‘ƒ∂¡øÏ≥µœµ¡–¥∞∏
| ƒÍº∂ | ∏þ÷–øŒ≥à | ƒÍº∂ | ≥ı÷–øŒ≥à |
| ∏þ“ª | ∏þ“ª√‚∑—øŒ≥ÃÕ∆ºˆ£° | ≥ı“ª | ≥ı“ª√‚∑—øŒ≥ÃÕ∆ºˆ£° |
| ∏þ∂˛ | ∏þ∂˛√‚∑—øŒ≥ÃÕ∆ºˆ£° | ≥ı∂˛ | ≥ı∂˛√‚∑—øŒ≥ÃÕ∆ºˆ£° |
| ∏þ»˝ | ∏þ»˝√‚∑—øŒ≥ÃÕ∆ºˆ£° | ≥ı»˝ | ≥ı»˝√‚∑—øŒ≥ÃÕ∆ºˆ£° |
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø»ÁÕº£¨∆Ω––Àƒ±þ–ŒABCD÷–£¨E£¨F «∂‘Ω«œþBD…œµƒ¡Ωµ„£¨»Áπ˚Ã̺”“ª∏ˆÃıº˛ π°˜ABE°’°˜CDF£¨‘ÚÃ̺”µƒÃıº˛≤ªƒÐ «( )
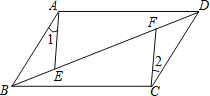
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø“—÷™£∫![]() ÷–£¨
÷–£¨![]() £¨«Û÷§£∫
£¨«Û÷§£∫![]() £¨œ¬√Ê–¥≥ˆø…‘À”√∑¥÷§∑®÷§√˜’‚∏ˆ√¸Ã‚µƒÀƒ∏ˆ≤Ω÷Ë£∫
£¨œ¬√Ê–¥≥ˆø…‘À”√∑¥÷§∑®÷§√˜’‚∏ˆ√¸Ã‚µƒÀƒ∏ˆ≤Ω÷Ë£∫
¢Ÿ°ý![]() £¨’‚”λ˝Ω«–Œƒ⁄Ω«∫ÕŒ™
£¨’‚”λ˝Ω«–Œƒ⁄Ω«∫ÕŒ™![]() √¨∂Ð,¢⁄“Ú¥ÀºŸ…Ë≤ª≥…¡¢£Æ°ý
√¨∂Ð,¢⁄“Ú¥ÀºŸ…Ë≤ª≥…¡¢£Æ°ý![]() ,¢€ºŸ…Ë‘⁄
,¢€ºŸ…Ë‘⁄![]() ÷–£¨
÷–£¨![]() ,¢Ð”…
,¢Ð”…![]() £¨µ√
£¨µ√![]() £¨º¥
£¨º¥![]() £Æ’‚Àƒ∏ˆ≤Ω÷Ë’˝»∑µƒÀ≥–Ú”¶ «£®°°°°£©
£Æ’‚Àƒ∏ˆ≤Ω÷Ë’˝»∑µƒÀ≥–Ú”¶ «£®°°°°£©
A.¢€¢Ð¢⁄¢ŸB.¢€¢Ð¢Ÿ¢⁄C.¢Ÿ¢⁄¢€¢ÐD.¢Ð¢€¢Ÿ¢⁄
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
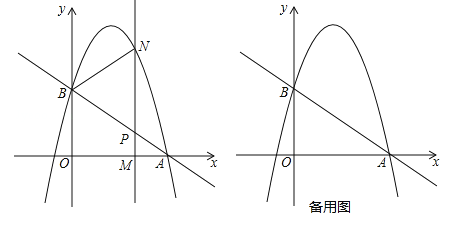
°æƒø°ø»ÁÕº£¨≈◊ŒÔœþy=©Å![]() +bx+cπ˝µ„A£®3£¨0£©£¨B£®0£¨2£©£ÆM£®m£¨0£©Œ™œþ∂ŒOA…œ“ª∏ˆ∂ص„£®µ„M”ε„A≤ª÷ÿ∫œ£©£¨π˝µ„M◊˜¥π÷±”⁄x÷·µƒ÷±œþ”Î÷±œþAB∫Õ≈◊ŒÔœþ∑÷±Ωª”⁄µ„P°¢N£Æ
+bx+cπ˝µ„A£®3£¨0£©£¨B£®0£¨2£©£ÆM£®m£¨0£©Œ™œþ∂ŒOA…œ“ª∏ˆ∂ص„£®µ„M”ε„A≤ª÷ÿ∫œ£©£¨π˝µ„M◊˜¥π÷±”⁄x÷·µƒ÷±œþ”Î÷±œþAB∫Õ≈◊ŒÔœþ∑÷±Ωª”⁄µ„P°¢N£Æ
£®1£©«Û÷±œþABµƒΩ‚Œˆ Ω∫Õ≈◊ŒÔœþµƒΩ‚Œˆ Ω£ª
£®2£©»Áπ˚µ„P «MNµƒ÷–µ„£¨ƒ«√¥«Û¥À ±µ„Nµƒ◊¯±Í£ª
£®3£©‘⁄∂‘≥∆÷·µƒ◊Û≤ý «∑ҥʑ⁄µ„M πÀƒ±þ–ŒOMPBµƒ√ʪ˝◊Ó¥Û£¨»Áπ˚¥Ê‘⁄«Ûµ„Mµƒ◊¯±Í£ª≤ª¥Ê‘⁄«ÎÀµ√˜¿Ì”…£Æ
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø»ÁÕº£¨‘⁄ ˝÷·…œ£¨µ„A±Ì æ1£¨œ÷Ω´µ„A—ÿ ˝÷·◊ˆ»Áœ¬“∆∂Ø£¨µ⁄“ª¥Œµ„AœÚ◊Û“∆∂Ø3∏ˆµ•Œª≥§∂»µΩ¥Ôµ„A1£¨µ⁄∂˛¥ŒΩ´µ„A1œÚ”““∆∂Ø6∏ˆµ•Œª≥§∂»µΩ¥Ôµ„A2£¨µ⁄»˝¥ŒΩ´µ„A2œÚ◊Û“∆∂Ø9∏ˆµ•Œª≥§∂»µΩ¥Ôµ„A3£¨∞¥’’’‚÷÷πʬ…œ¬»•£¨µ⁄n¥Œ“∆∂ØµΩµ„An£¨»Áπ˚µ„An£¨”Α≠µ„µƒæý¿Î≤ª…Ÿ”⁄20£¨ƒ«√¥nµƒ◊Ó–°÷µ «£® £©

A. 11B. 12C. 13D. 20
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
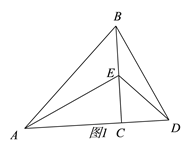
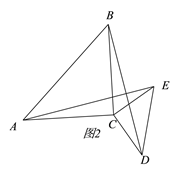
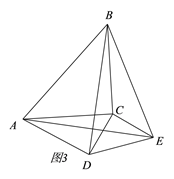
°æƒø°ø°˜ACB∫Õ°˜ECDæ˘Œ™µ»—¸÷±Ω«»˝Ω«–Œ£¨°œACB=°œECD=90°„.
£®1£©»ÁÕº1£¨µ„E‘⁄BC…œ£¨‘Úœþ∂ŒAE∫ÕBD”–‘ı—˘µƒπÿœµ£ø«Î÷±Ω”–¥≥ˆΩ·¬€£®≤ª–Ë÷§√˜£©£ª
£®2£©»ÙΩ´°˜DCE»∆µ„C–˝◊™“ª∂®µƒΩ«∂»µ√Õº2£¨‘Ú£®1£©÷–µƒΩ·¬€ «∑Ò»‘»ª≥…¡¢£ø«ÎÀµ√˜¿Ì”…£ª
£®3£©µ±°˜DCE–˝◊™µΩ π°œADC=90°„ ±£¨»ÙAC=5£¨CD=3£¨«ÛBEµƒ≥§.
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
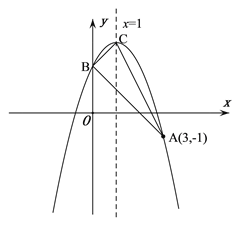
°æƒø°ø»ÁÕº£¨≈◊ŒÔœþ![]() µƒ∂•µ„Œ™C£¨∂‘≥∆÷·Œ™÷±œþ
µƒ∂•µ„Œ™C£¨∂‘≥∆÷·Œ™÷±œþ![]() £¨«“æ≠π˝µ„A(3,£≠1)£¨”Îy÷·Ωª”⁄µ„B.
£¨«“æ≠π˝µ„A(3,£≠1)£¨”Îy÷·Ωª”⁄µ„B.
£®1£©«Û≈◊ŒÔœþµƒΩ‚Œˆ Ω£ª
£®2£©≈–∂œ°˜ABCµƒ–Œ◊¥£¨≤¢Àµ√˜¿Ì”…£ª
£®3£©æ≠π˝µ„Aµƒ÷±œþΩª≈◊ŒÔœþ”⁄µ„P£¨Ωªx÷·”⁄µ„Q£¨»Ù![]() £¨ ‘«Û≥ˆµ„Pµƒ◊¯±Í.
£¨ ‘«Û≥ˆµ„Pµƒ◊¯±Í.
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
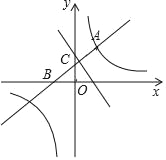
°æƒø°ø»ÁÕº£¨÷±œþy=x+b”ÎÀ´«˙œþy=![]() £®k «≥£ ˝£¨k°Ÿ0£©‘⁄µ⁄“ªœÛœÞƒ⁄Ωª”⁄µ„A£®1£¨2£©£¨«“”Îx÷·°¢y÷·∑÷±Ωª”⁄B£¨C¡Ωµ„£Æµ„P‘⁄x÷·£Æ
£®k «≥£ ˝£¨k°Ÿ0£©‘⁄µ⁄“ªœÛœÞƒ⁄Ωª”⁄µ„A£®1£¨2£©£¨«“”Îx÷·°¢y÷·∑÷±Ωª”⁄B£¨C¡Ωµ„£Æµ„P‘⁄x÷·£Æ
£®1£©«Û÷±œþ∫ÕÀ´«˙œþµƒΩ‚Œˆ Ω£ª
£®2£©»Ù°˜BCPµƒ√ʪ˝µ»”⁄2£¨«ÛPµ„µƒ◊¯±Í£ª
£®3£©«ÛPA+PCµƒ◊Ó∂Ãæý¿Î£Æ
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°øºŒ‰ø◊º±∏ÕÍ≥…ƒø£∫ªØºÚ£∫![]() £¨∑¢œ÷œµ ˝°∞
£¨∑¢œ÷œµ ˝°∞![]() °±”°À¢≤ª«Â≥˛£Æ
°±”°À¢≤ª«Â≥˛£Æ
£®1£©À˚∞—°∞![]() °±≤¬≥…3£¨«Îƒ„ªØºÚ£∫£®3x2+6x+8£©®C£®6x+5x2+2£©£ª
°±≤¬≥…3£¨«Îƒ„ªØºÚ£∫£®3x2+6x+8£©®C£®6x+5x2+2£©£ª
£®2£©À˚¬Ë¬ËÀµ£∫°∞ƒ„≤¬¥Ì¡À£¨Œ“ø¥µΩ∏√±Í◊º¥∞∏µƒΩ·π˚ «≥£ ˝£Æ°±Õ®π˝º∆À„Àµ√˜‘≠Â÷–°∞![]() °± «º∏£ø
°± «º∏£ø
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
π˙º —ß–£”≈—° - ¡∑œ∞≤·¡–±Ì - ‘¡–±Ì
∫˛±± °ª•¡™Õ¯Œ•∑®∫Õ≤ª¡º–≈œ¢æŸ±®∆Ωî | Õ¯…œ”–∫¶–≈œ¢æŸ±®◊®«¯ | µÁ–≈’©∆≠柱®◊®«¯ | …Ê¿˙ ∑–ÈŒÞ÷˜“”–∫¶–≈œ¢æŸ±®◊®«¯ | …Ê∆Û«÷»®æŸ±®◊®«¯
Œ•∑®∫Õ≤ª¡º–≈œ¢æŸ±®µÁª∞£∫027-86699610 柱®” œ‰£∫58377363@163.com