
【题目】△ACB和△ECD均为等腰直角三角形,∠ACB=∠ECD=90°.
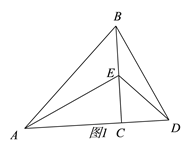
(1)如图1,点E在BC上,则线段AE和BD有怎样的关系?请直接写出结论(不需证明);
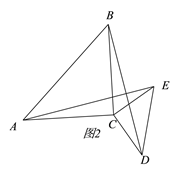
(2)若将△DCE绕点C旋转一定的角度得图2,则(1)中的结论是否仍然成立?请说明理由;
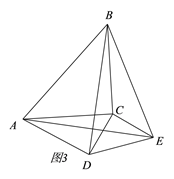
(3)当△DCE旋转到使∠ADC=90°时,若AC=5,CD=3,求BE的长.
【答案】(1)AE=BD,AE⊥BD ;(2)见解析;(3)![]()
【解析】分析:(1)延长AE交BD于F,由△AEC≌△BDC,可得AE=BD,再利用同角的余角相等,可得出AE⊥BD ;(2)不发生变化,只要证明△AEC≌△BDC,推出AE=BD,∠EAC=∠DBC,由∠EAC+∠AFC =90°,∠AFC=∠BFG,可得∠BGF=90°,从而得证;(3)过B作BM⊥EC于M,则∠M=90°,在RT△ACD中利用勾股定理可得AD=4,再利用△BCM≌△ACD,得出CM=CD=3, BM=AD=4,在△BME中利用勾股定理即可求出结果.
本题解析:
(1)AE=BD,AE⊥BD ;
(2)(1)中的结论仍然成立,理由如下:
∵△ACB和△ECD均为等腰直角三角形,∠ACB=∠ECD=90°
∴AC=BC, ∠ACE=∠BCD,EC=DC
∴△ACE≌△BCD(SAS), ∴AE=BD, ∠EAC=∠DBC
∵∠EAC+∠AFC =90°,∠AFC=∠BFG
∴∠DBC+∠BFG=90°, ∴∠BGF=90°,
∴AE⊥BD
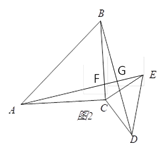
(3) 过B作BM⊥EC于M,则∠M=90°
∵∠ADC=90°,AC=5,CD=3,∴AD=![]()
∵∠ACB=∠ECD=90°, ∴∠CBE+∠ACD=180°
∵∠CBE+∠BCM=180°, ∴∠BCM=∠ACD
∵∠M=∠ADC=90°, AC=BC
∴△BCM≌△ACD(AAS), ∴CM=CD=3, BM=AD=4
∵CE=CD=3,∴EM=6,
∴BE=![]()


科目:初中数学 来源: 题型:
【题目】如图1,将正方形ABCD置于平面直角坐标系中,其中AD边在x轴上,其余各边均与坐标轴平行,直线l:y=x﹣3沿x轴的负方向以每秒1个单位的速度平移,在平移的过程中,该直线被正方形ABCD的边所截得的线段长为m,平移的时间为t(秒),m与t的函数图象如图2所示,则图2中b的值为( )
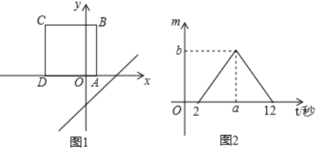
A. 5![]() B. 4
B. 4![]() C. 3
C. 3![]() D. 2
D. 2![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知等边△ABC的边长为![]() ,D是AB上的动点,过D作DE⊥AC于点E,过E作EF⊥BC于点F,过F作FG⊥AB于点G.当G与D重合时,AD的长是( )
,D是AB上的动点,过D作DE⊥AC于点E,过E作EF⊥BC于点F,过F作FG⊥AB于点G.当G与D重合时,AD的长是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在![]() 中,
中,![]() 垂直平分
垂直平分![]() ,分别交
,分别交![]() 、
、![]() 于点
于点![]() 、
、![]() ,
,![]() 垂直平分
垂直平分![]() ,分别交
,分别交![]() ,
,![]() 于点
于点![]() 、
、![]() .
.
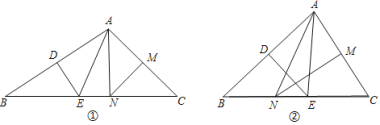
⑴如图①,若![]() ,求
,求![]() 的度数;
的度数;
⑵如图②,若![]() ,求
,求![]() 的度数;
的度数;
⑶若![]()
![]() ,直接写出用
,直接写出用![]() 表示
表示![]() 大小的代数式.
大小的代数式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】现有一个种植总面积为![]() 的矩形塑料温棚,分垄间隔套种草莓和西红柿共
的矩形塑料温棚,分垄间隔套种草莓和西红柿共![]() 垄,种植的草莓或西红柿单种农作物的总垄数不低于8垄,又不超过
垄,种植的草莓或西红柿单种农作物的总垄数不低于8垄,又不超过![]() 垄(垄数为正整数),它们的占地面积、产量、利润分别如下:
垄(垄数为正整数),它们的占地面积、产量、利润分别如下:
⑴若设草莓共种植了![]() 垄,通过计算说明共有几种种植方案?分别是哪几种?
垄,通过计算说明共有几种种植方案?分别是哪几种?
⑵在这几种种植方案中,哪种方案获得的利润最大?最大利润是多少?
占地面积(m2/垄) | 产量(千克/垄) | 利润(元/千克) | |
西红柿 | 32 | 160 | 1.0 |
草莓 | 15 | 50 | 1.6 |
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知∠1=∠2,DE⊥BC,AB⊥BC,求证:∠A=∠3.
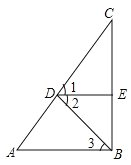
证明:∵ DE⊥BC,AB⊥BC(已知)
∴∠DEC=∠ABC=90°( )
∴DE∥AB(_________ ___)
∴∠2=____ (__________ ___________)
∠1= (____________ _________)
又∵∠1=∠2(_____________________)
∴∠A=∠3(_____________________)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD中,点E,F分别在边AB与CD上,点G、H在对角线AC上,AG=CH,BE=DF.
(1)求证:四边形EGFH是平行四边形;
(2)若EG=EH,AB=8,BC=4.求AE的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线y=-x+m与y=nx+4n(n≠0)的交点的横坐标为-2.则下列结论:①m<0,n>0;②直线y=nx+4n一定经过点(-4,0);③m与n满足m=2n-2;④当x>-2时,nx+4n>-x+m,其中正确结论的个数是( )
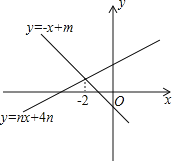
A. 1个B. 2个C. 3个D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在口ABCD中,AE⊥BC于点E,AF⊥CD于点F,且AE=3cm,AF=5cm.若口ABCD的周长为32cm,则口ABCD的面积为( )
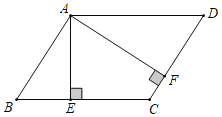
A. 24cm2B. 30cm2C. 64cm2D. 108cm2
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com