
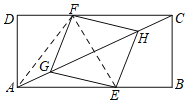
【题目】如图,矩形ABCD中,点E,F分别在边AB与CD上,点G、H在对角线AC上,AG=CH,BE=DF.
(1)求证:四边形EGFH是平行四边形;
(2)若EG=EH,AB=8,BC=4.求AE的长.

【答案】(1)见解析;(2)AE=5.
【解析】
(1)依据矩形的性质,即可得出△AEG≌△CFH,进而得到GE=FH,∠CHF=∠AGE,由∠FHG=∠EGH,可得FH∥GE,即可得到四边形EGFH是平行四边形;
(2)由菱形的性质,即可得到EF垂直平分AC,进而得出AF=CF=AE,设AE=x,则FC=AF=x,DF=8-x,依据Rt△ADF中,AD2+DF2=AF2,即可得到方程,即可得到AE的长.
(1)∵矩形ABCD中,AB∥CD,
∴∠FCH=∠EAG,
又∵CD=AB,BE=DF,
∴CF=AE,
又∵CH=AG,
∴△AEG≌△CFH,
∴GE=FH,∠CHF=∠AGE,
∴∠FHG=∠EGH,
∴FH∥GE,
∴四边形EGFH是平行四边形;
(2)如图,连接EF,AF,
∵EG=EH,四边形EGFH是平行四边形,
∴四边形GFHE为菱形,
∴EF垂直平分GH,
又∵AG=CH,
∴EF垂直平分AC,
∴AF=CF=AE,
设AE=x,则FC=AF=x,DF=8-x,
在Rt△ADF中,AD2+DF2=AF2,
∴42+(8-x)2=x2,
解得x=5,
∴AE=5.


科目:初中数学 来源: 题型:
【题目】某水果店在两周内,将标价为10元/斤的某种水果,经过两次降价后的价格为8.1元/斤,并且两次降价的百分率相同.
(1)求该种水果每次降价的百分率;
(2)从第一次降价的第1天算起,第x天(x为整数)的售价、销量及储存和损耗费用的相关信息如表所示.已知该种水果的进价为4.1元/斤,设销售该水果第x(天)的利润为y(元),求y与x(1≤x<15)之间的函数关系式,并求出第几天时销售利润最大?
时间x(天) | 1≤x<9 | 9≤x<15 | x≥15 |
售价(元/斤) | 第1次降价后的价格 | 第2次降价后的价格 | |
销量(斤) | 80﹣3x | 120﹣x | |
储存和损耗费用(元) | 40+3x | 3x2﹣64x+400 | |
(3)在(2)的条件下,若要使第15天的利润比(2)中最大利润最多少127.5元,则第15天在第14天的价格基础上最多可降多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
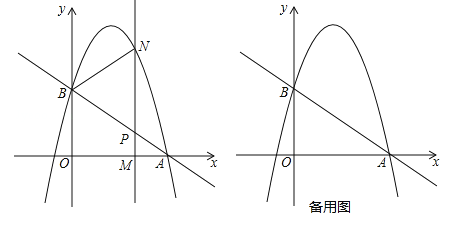
【题目】如图,抛物线y=﹣![]() +bx+c过点A(3,0),B(0,2).M(m,0)为线段OA上一个动点(点M与点A不重合),过点M作垂直于x轴的直线与直线AB和抛物线分别交于点P、N.
+bx+c过点A(3,0),B(0,2).M(m,0)为线段OA上一个动点(点M与点A不重合),过点M作垂直于x轴的直线与直线AB和抛物线分别交于点P、N.
(1)求直线AB的解析式和抛物线的解析式;
(2)如果点P是MN的中点,那么求此时点N的坐标;
(3)在对称轴的左侧是否存在点M使四边形OMPB的面积最大,如果存在求点M的坐标;不存在请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
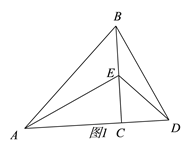
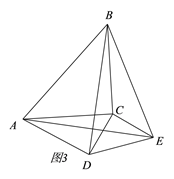
【题目】△ACB和△ECD均为等腰直角三角形,∠ACB=∠ECD=90°.
(1)如图1,点E在BC上,则线段AE和BD有怎样的关系?请直接写出结论(不需证明);
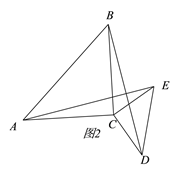
(2)若将△DCE绕点C旋转一定的角度得图2,则(1)中的结论是否仍然成立?请说明理由;
(3)当△DCE旋转到使∠ADC=90°时,若AC=5,CD=3,求BE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
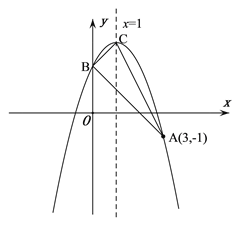
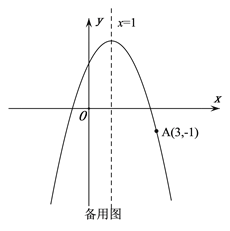
【题目】如图,抛物线![]() 的顶点为C,对称轴为直线
的顶点为C,对称轴为直线![]() ,且经过点A(3,-1),与y轴交于点B.
,且经过点A(3,-1),与y轴交于点B.
(1)求抛物线的解析式;
(2)判断△ABC的形状,并说明理由;
(3)经过点A的直线交抛物线于点P,交x轴于点Q,若![]() ,试求出点P的坐标.
,试求出点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
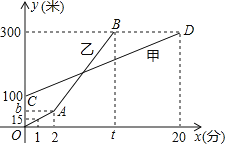
【题目】甲乙两人同时登山,甲乙两人距地面的高度![]() (米
(米![]() 与登山时间
与登山时间![]() (分
(分![]() 之间的函数图象如图所示,根据图象所提供的信息解答下列问题:
之间的函数图象如图所示,根据图象所提供的信息解答下列问题:
(1)甲登山的速度是 米![]() 分钟,乙在
分钟,乙在![]() 地提速时距地面的高度
地提速时距地面的高度![]() 为 米;
为 米;
(2)直接写出甲距地面高度![]() (米
(米![]() 和
和![]() (分
(分![]() 之间的函数关系式;
之间的函数关系式;
(3)若乙提速后,乙的速度是甲登山速度的3倍.请问登山多长时间时,乙追上了甲,此时乙距![]() 地的高度为多少米?
地的高度为多少米?
查看答案和解析>>
科目:初中数学 来源: 题型:
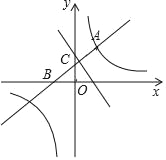
【题目】如图,直线y=x+b与双曲线y=![]() (k是常数,k≠0)在第一象限内交于点A(1,2),且与x轴、y轴分别交于B,C两点.点P在x轴.
(k是常数,k≠0)在第一象限内交于点A(1,2),且与x轴、y轴分别交于B,C两点.点P在x轴.
(1)求直线和双曲线的解析式;
(2)若△BCP的面积等于2,求P点的坐标;
(3)求PA+PC的最短距离.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为给同学们创造更好的读书条件,学校准备新建一个长度为L的度数长廊,并准备用若干块带有花纹和没有花纹的两种规格、大小相同的正方形地面砖搭配在一起,按如图所示的规律拼成图案铺满长廊,已知每个小正方形地面砖的边长均为0.6m.

(1)按图示规律,第一图案的长度L1= m;第二个图案的长度L2= m.
(2)请用代数式表示带有花纹的地面砖块数n与走廊的长度Ln之间的关系.
(3)当走廊的长度L为36.6m时,请计算出所需带有花纹图案的瓷砖的块数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】今年4月23日是第23个“世界读书日”,也是江苏省第四个法定的全民阅读日。由市文明办、市全民阅读办、市文广新局等单位联合主办的“2018无锡市第三个全民阅读日”系列活动即将启动。某校围绕学生日人均阅读时间这一问题,对初二学生进行随机抽样调查.如图是根据调查结果绘制成的统计图(不完整),请你根据图中提供的信息解答下列问题:
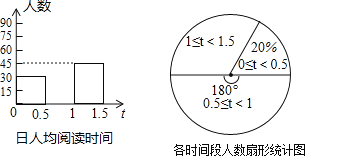
(1)本次抽样调查的样本容量是 .
(2)请将条形统计图补充完整.
(3)在扇形统计图中,计算出日人均阅读时间在1~1.5小时对应的圆心角是 度.
(4)根据本次抽样调查,试估计我市12000名初二学生中日人均阅读时间在0.5~1.5小时的多少人.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com