
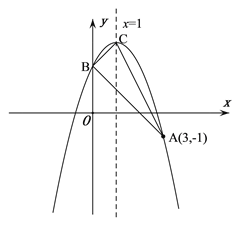
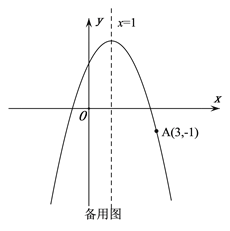
【题目】如图,抛物线![]() 的顶点为C,对称轴为直线
的顶点为C,对称轴为直线![]() ,且经过点A(3,-1),与y轴交于点B.
,且经过点A(3,-1),与y轴交于点B.
(1)求抛物线的解析式;
(2)判断△ABC的形状,并说明理由;
(3)经过点A的直线交抛物线于点P,交x轴于点Q,若![]() ,试求出点P的坐标.
,试求出点P的坐标.
【答案】(1)![]() ;(2)△ABC是直角三角形,理由见解析;(3)点P的坐标为
;(2)△ABC是直角三角形,理由见解析;(3)点P的坐标为![]() 、
、![]() 、
、![]() 或
或![]()
【解析】分析:(1)利用待定系数法,联立方程组即可解得;(2)利用解析式![]() ,可得B(0,2),C(1,3),再由A(3,-1),求出AB,AC,BC ,利用勾股定理的逆定理即可得出结果;(3)分两种情况讨论:当点Q在线段AP上时,当点Q在PA延长线上时,可得点P的坐标.
,可得B(0,2),C(1,3),再由A(3,-1),求出AB,AC,BC ,利用勾股定理的逆定理即可得出结果;(3)分两种情况讨论:当点Q在线段AP上时,当点Q在PA延长线上时,可得点P的坐标.
本题解析:
(1)由题意得: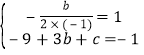 , 解得:
, 解得:![]()
∴抛物线的解析式为![]()
(2)由![]() 得:当
得:当![]() 时,y=2.,∴
时,y=2.,∴![]() ,由
,由![]() 得,
得,![]()
∵A(3,-1),∴![]() ,∴
,∴![]()
∴∠ABC=90°,∴△ABC是直角三角形.
(3)①如图,当点Q在线段AP上时,过点P作PE⊥x轴于点E,AD⊥x轴于点D

∵![]() ,∴PA=2AQ,∴PQ=AQ
,∴PA=2AQ,∴PQ=AQ
∵PE∥AD,∴△PQE∽△AQD,
∴![]() ,∴PE=AD=1
,∴PE=AD=1
由![]() 得:
得:![]()
∴P![]() 或
或![]()
②如图,当点Q在PA延长线上时,过点P作PE⊥x轴于点E,AD⊥x轴于点D
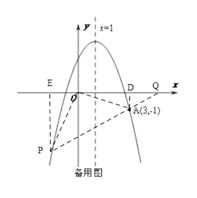
∵![]() ,∴PA=2AQ,∴PQ=3AQ
,∴PA=2AQ,∴PQ=3AQ
∵PE∥AD,∴△PQE∽△AQD,
∴![]() ,∴PE=3AD=3
,∴PE=3AD=3
由![]() 得:
得:![]() ,∴P
,∴P![]() 或
或![]() .
.
综上可知:点P的坐标为![]() 、
、![]() 、
、![]() 或
或![]()


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
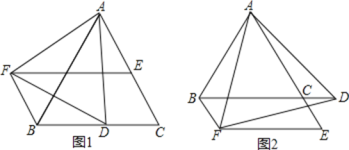
【题目】已知![]() 是等边三角形,D是BC边上的一个动点
是等边三角形,D是BC边上的一个动点![]() 点D不与B,C重合
点D不与B,C重合![]() 是以AD为边的等边三角形,过点F作BC的平行线交射线AC于点E,连接BF.
是以AD为边的等边三角形,过点F作BC的平行线交射线AC于点E,连接BF.
![]() 如图1,求证:
如图1,求证:![]() ≌
≌![]() ;
;
![]() 请判断图1中四边形BCEF的形状,并说明理由;
请判断图1中四边形BCEF的形状,并说明理由;
![]() 若D点在BC边的延长线上,如图2,其它条件不变,请问
若D点在BC边的延长线上,如图2,其它条件不变,请问![]() 中结论还成立吗?如果成立,请说明理由.
中结论还成立吗?如果成立,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某体育用品商场预测某品牌运动服能够畅销,就用32000元购进了一批这种运动服,上市后很快脱销,商场又用68000元购进第二批这种运动服,所购数量是第一批购进数量的2倍,但每套进价多了10元.
(1)该商场两次共购进这种运动服多少套?
(2)如果这两批运动服每套的售价相同,且全部售完后总利润不低于20%,那么每套售价至少是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】现有一个种植总面积为![]() 的矩形塑料温棚,分垄间隔套种草莓和西红柿共
的矩形塑料温棚,分垄间隔套种草莓和西红柿共![]() 垄,种植的草莓或西红柿单种农作物的总垄数不低于8垄,又不超过
垄,种植的草莓或西红柿单种农作物的总垄数不低于8垄,又不超过![]() 垄(垄数为正整数),它们的占地面积、产量、利润分别如下:
垄(垄数为正整数),它们的占地面积、产量、利润分别如下:
⑴若设草莓共种植了![]() 垄,通过计算说明共有几种种植方案?分别是哪几种?
垄,通过计算说明共有几种种植方案?分别是哪几种?
⑵在这几种种植方案中,哪种方案获得的利润最大?最大利润是多少?
占地面积(m2/垄) | 产量(千克/垄) | 利润(元/千克) | |
西红柿 | 32 | 160 | 1.0 |
草莓 | 15 | 50 | 1.6 |
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】观察下列两个等式:![]() ,
,![]() ,给出定义如下:我们称使等式a﹣b=ab+1的成立的一对有理数a,b为“共生有理数对”,记为(a,b),如:数对
,给出定义如下:我们称使等式a﹣b=ab+1的成立的一对有理数a,b为“共生有理数对”,记为(a,b),如:数对![]() ,
,![]() ,都是“共生有理数对”.
,都是“共生有理数对”.
(1)数对![]() ,
,![]() 中是“共生有理数对”的是 ;
中是“共生有理数对”的是 ;
(2)若(m,n)是“共生有理数对”,则(﹣n,﹣m) “共生有理数对”(填“是”或“不是”);
(3)请再写出一对符合条件的“共生有理数对”为 ;(注意:不能与题目中已有的“共生有理数对”重复)
(4)若(a,3)是“共生有理数对”,求a的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD中,点E,F分别在边AB与CD上,点G、H在对角线AC上,AG=CH,BE=DF.
(1)求证:四边形EGFH是平行四边形;
(2)若EG=EH,AB=8,BC=4.求AE的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】生活中,有人喜欢把传送的便条折成![]() 形状,折叠过程是这样的(阴影部分表示纸条的反面):如果由信纸折成的长方形纸条(图①)长为
形状,折叠过程是这样的(阴影部分表示纸条的反面):如果由信纸折成的长方形纸条(图①)长为![]() ,宽为
,宽为![]() ,分别回答下列问题:
,分别回答下列问题:
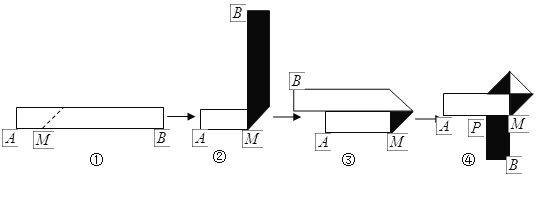
(1)为了保证能折成图④的形状(即纸条两端均超出点![]() ),试求
),试求![]() 的取值范围.
的取值范围.
(2)如果不但要折成图④的形状,而且为了美观,希望纸条两端超出点![]() 的长度相等,即最终图形是轴对称图形,试求在开始折叠时起点
的长度相等,即最终图形是轴对称图形,试求在开始折叠时起点![]() 与点
与点![]() 的距离(用
的距离(用![]() 表示)
表示)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“中国汉字听写大会”是由中央电视台和国家语言文字工作委员会联合主办的节目,希望通过节目的播出,能吸引更多的人关注对汉字文化的学习.某校也开展了一次“汉字听写”比赛,每位参赛学生听写40个汉字.比赛结束后随机抽取部分学生的听写结果,按听写正确的汉字个数x绘制成了以下不完整的统计图.
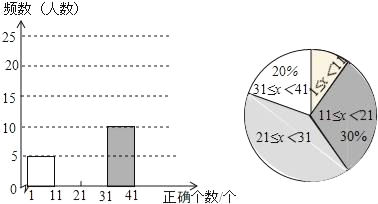
根据以上信息回答下列问题:
(1)本次共随机抽取了 名学生进行调查,听写正确的汉字个数x在 范围的人数最多;
(2)补全频数分布直方图;
(3)各组的组中值如下表所示.若用各组的组中值代表各组每位学生听写正确的汉字个数,求被调查学生听写正确的汉字个数的平均数;
听写正确的汉字个数x | 组中值 |
1≤x<11 | 6 |
11≤x<21 | 16 |
21≤x<31 | 26 |
31≤x<41 | 36 |
(4)该校共有1350名学生,如果听写正确的汉字个数不少于21个定为良好,请你估计该校本次“汉字听写”比赛达到良好的学生人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为鼓励市民节约用水,某市自来水公司对每户用水量进行了分段计费,每户每月用水量在规定吨数以下的收费标准相同,规定吨数以上的超过部分收费相同.如表是小明家1-4月
用水量和交费情况,根据表格提供的数据,回答:
月份 | 一 | 二 | 三 | 四 |
用水量(吨) | 6 | 7 | 12 | 15 |
水费(元) | 12 | 14 | 28 | 37 |
(1)该市规定用水量为 吨,规定用量内的收费标准是 元/吨,超过部分的收费标准是 元/吨。
(2)若小明家5月份用水20吨,则应缴水费 元。
(3)若小明家6月份应交水费46元,则6月份他们家的用水量是多少吨?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com