
【题目】计算:
(1)﹣28﹣(﹣15)+(﹣17)﹣(+5)
(2)(﹣72)×2![]()
(3)![]()
(4)![]()
(5)3m2﹣mn﹣2m2+4mn
(6)(3x2﹣xy﹣2y2)﹣2(x2+xy﹣2y2)
【答案】(1)-35;(2)-20;(3)-21;(4)![]() ;(5)m2+3mn;(6)x2﹣3xy+2y2.
;(5)m2+3mn;(6)x2﹣3xy+2y2.
【解析】
(1)原式利用减法法则变形,计算即可求出值;
(2)原式从左到右依次计算即可求出值;
(3)原式先计算乘方运算,再计算乘除运算即可求出值;
(4)原式先计算括号中的运算,再计算乘除运算即可求出值;
(5)原式合并同类项即可得到结果;
(6)原式去括号合并即可得到结果.
(1)原式=﹣28+15﹣17﹣5=﹣45+10=﹣35;
(2)原式=﹣72×![]() ×
×![]() ×
×![]() =﹣20;
=﹣20;
(3)原式=﹣16﹣6﹣14+15=﹣21;
(4)原式=(﹣1+![]() )×(2+27)×(﹣2)=﹣
)×(2+27)×(﹣2)=﹣![]() ×(﹣58)=
×(﹣58)=![]() ;
;
(5)原式=3m2﹣2m2﹣mn+4mn=m2+3mn;
(6)原式=3x2﹣xy﹣2y2﹣2x2﹣2xy+4y2=x2﹣3xy+2y2.


 作业辅导系列答案
作业辅导系列答案科目:初中数学 来源: 题型:
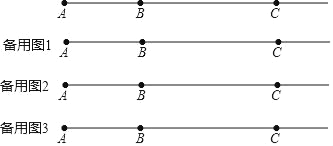
【题目】如图,直线l上依次有三点A、B、C,且AB=8、BC=16,点P为射线AB上一动点,将线段AP进行翻折得到线段PA′(点A落在直线l上点A′处、线段AP上的所有点与线段PA′上的点对应).
(1)若翻折后A′C=2,则翻折前线段AP= .
(2)若点P在线段BC上运动,点M为线段A′C的中点,直接写出线段PM的长度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】学习有理数的乘法后,老师给同学们这样一道题目:计算:49![]() ×(﹣5),看谁算的又快又对,有两位同学的解法如下:
×(﹣5),看谁算的又快又对,有两位同学的解法如下:
小明:原式=﹣![]() ×5=﹣
×5=﹣![]() =﹣249
=﹣249![]() ;
;
小军:原式=(49+![]() )×(﹣5)=49×(﹣5)+
)×(﹣5)=49×(﹣5)+![]() ×(﹣5)=﹣249
×(﹣5)=﹣249![]() ;
;
(1)对于以上两种解法,你认为谁的解法较好?
(2)上面的解法对你有何启发,你认为还有更好的方法吗?如果有,请把它写出来;
(3)用你认为最合适的方法计算:19![]() ×(﹣8)
×(﹣8)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】△ABC在平面直角坐标系中的位置如图所示,其中每个小正方形的边长为1个单位长度.按要求作图: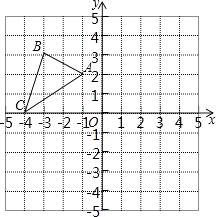
(1)画出△ABC关于原点O的中心对称图形△A1B1C1;
(2)画出将△ABC绕点A逆时针旋转90°得到△AB2C2 ,
(3)△A1B1C1中顶点A1坐标为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】问题提出 平面内不在同一条直线上的三点确定一个面,那么平面内的四点(任意三点均不在同一直线上),能否在同一个面上呢?
初步思考
设不在同一条直线上的三点A、B、C确定的圆为⊙O.
(1)当C、D在线段AB的同侧时. 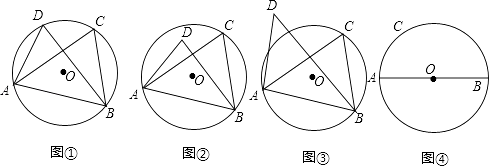
如图①,若点D在⊙O上,此时有∠ACB=∠ADB,理由是 .
如图②,若点D在⊙O内,此时有∠ACB∠ADB;
如图③,若点D在⊙O外,此时有∠ACB∠ADB(填“=”、“>”、“<”)
由上面的探究,请直接写出A、B、C、D四点在同一个圆上的条件: .
类比学习
(2)仿照上面的探究思路,请探究:当C、D在线段AB的异侧时的情形. 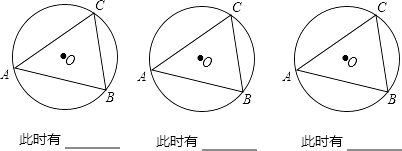
由上面的探究,请用文字语言直接写出A、B、C、D四点在同一个圆上的条件: .
拓展延伸
(3)如何过圆上一点,仅用没有刻度的直尺,作出已知直径的垂线? 已知:如图,AB是⊙O的直径,点C在⊙O上,求作:CN⊥AB
作法:①连接CA、CB
②在CB上任取异于B、C的一点D,连接DA,DB;
③DA与CB相交于E点,延长AC、BD,交于F点;
④连接F、E并延长,交直径AB与M;
⑤连接D、M并延长,交⊙O于N,连接CN,则CN⊥AB.
请安上述作法在图④中作图,并说明CN⊥AB的理由.(提示:可以利用(2)中的结论)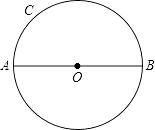
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,甲、乙两艘轮船同时从港口O出发,甲轮船以20海里/时的速度向南偏东45°方向航行,乙轮船向南偏西45°方向航行.已知它们离开港口O两小时后,两艘轮船相距50海里,求乙轮船平均每小时航行多少海里?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①是一个直角三角形纸片,∠A=30°,将其折叠,使点C落在斜边上的点C处,折痕为BD,如图②,再将②沿DE折叠,使点A落在DC′的延长线上的点A′处,如图③,若折痕DE的长是![]() cm,则BC的长是( )
cm,则BC的长是( )
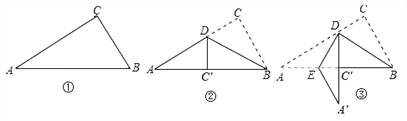
A. 3cm B. 4cm C. 5cm D. 6cm
查看答案和解析>>
科目:初中数学 来源: 题型:
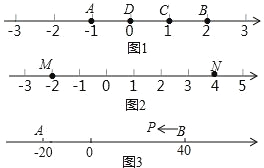
【题目】A、B、C 为数轴上三点,若点 C 到点 A 的距离是点 C 到点 B 的距离的 2倍,则称点 C 是(A,B)的奇异点,例如图 1 中,点 A 表示的数为﹣1,点B 表示的数为 2,表示 1 的点 C 到点 A 的距离为 2,到点 B 的距离为 1,则点C 是(A,B)的奇异点,但不是(B,A)的奇异点.
(1)在图 1 中,直接说出点 D 是(A,B)还是(B,C)的奇异点;
(2)如图 2,若数轴上 M、N 两点表示的数分别为﹣2 和 4,(M,N)的奇异点 K 在 M、N 两点之间,请求出 K 点表示的数;
(3)如图 3,A、B 在数轴上表示的数分别为﹣20 和 40,现有一点 P 从点 B 出发,向左运动.
①若点 P 到达点 A 停止,则当点 P 表示的数为多少时,P、A、B 中恰有一个点为其余两点的奇异点?
②若点 P 到达点 A 后继续向左运动,是否存在使得 P、A、B 中恰有一个点为其余两点的奇异点的情况?若存在,请直接写出此时 PB 的距离;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知点O到△ABC的两边AB,AC所在直线的距离相等,且OB=OC.
(1)如图①,若点O在边BC上,求证:AB=AC;
(2)如图②,若点O在△ABC的内部,求证:AB=AC;
(3)若点O在△ABC的外部,AB=AC成立吗?请画图表示.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com