
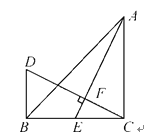
【题目】如图①是一个直角三角形纸片,∠A=30°,将其折叠,使点C落在斜边上的点C处,折痕为BD,如图②,再将②沿DE折叠,使点A落在DC′的延长线上的点A′处,如图③,若折痕DE的长是![]() cm,则BC的长是( )
cm,则BC的长是( )
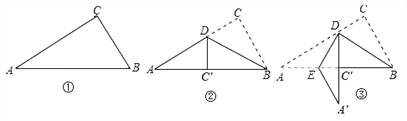
A. 3cm B. 4cm C. 5cm D. 6cm
【答案】B
【解析】分析:先根据在一个直角三角形纸片,∠A=30°,根据翻折图形的性质可得:
∠DBA=30°, ∠ADC’=60°, ∠A‘DE=30°,所以∠BDE=90°,在Rt△BDE中, ∠DBE=30°,DE=![]() ,根据30°角所对直角边等于斜边的一半,可得:BE=
,根据30°角所对直角边等于斜边的一半,可得:BE=![]() ,根据勾股定理可得:BD=
,根据勾股定理可得:BD=![]() , 在Rt△DBC中, ∠DBC=30°,DB=
, 在Rt△DBC中, ∠DBC=30°,DB=![]() ,根据30°角所对直角边等于斜边的一半,可得:DC=
,根据30°角所对直角边等于斜边的一半,可得:DC=![]() ,根据勾股定理可得:BC=
,根据勾股定理可得:BC=![]() .
.
详解: 因为∠A=30°,根据翻折图形的性质可得:
∠DBA=30°, ∠ADC’=60°, ∠A‘DE=30°,
所以∠BDE=90°,
在Rt△BDE中, 因为∠DBE=30°,DE=![]() ,
,
所以BE=![]() ,
,
根据勾股定理可得:BD=![]() ,
,
在Rt△DBC中, ∠DBC=30°,DB=![]() ,根
,根
所以DC=![]() ,
,
根据勾股定理可得:BC=![]() .
.
故选B.


科目:初中数学 来源: 题型:
【题目】已知A=2a2+3ab﹣2a﹣1,B=﹣a2+![]() ab+
ab+![]() .
.
(1)a=﹣1,b=﹣2时,求4A﹣(3A﹣2B)的值;
(2)若(1)中式子的值与a的取值无关,求b的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是二次函数y=ax2+bx+c图象的一部分,图象过点A(﹣3,0),对称轴为直线x=﹣1,给出四个结论,其中正确结论是( ) 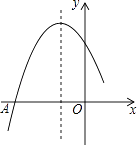
A.b2<4ac
B.2a+b=0
C.a+b+c>0
D.若点B( ![]() ,y1)、C(
,y1)、C( ![]() ,y2)为函数图象上的两点,则y1<y2
,y2)为函数图象上的两点,则y1<y2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】计算:
(1)﹣28﹣(﹣15)+(﹣17)﹣(+5)
(2)(﹣72)×2![]()
(3)![]()
(4)![]()
(5)3m2﹣mn﹣2m2+4mn
(6)(3x2﹣xy﹣2y2)﹣2(x2+xy﹣2y2)
查看答案和解析>>
科目:初中数学 来源: 题型:
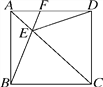
【题目】在正方形ABCD中,AC为对角线,点E为AC上一点,连接EB,ED.
(1)求证:△BEC≌△DEC;
(2)延长BE交AD于点F,当∠BED=120°时,求∠EFD的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
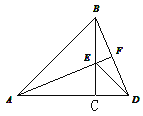
【题目】在△ABC和△DEC中,∠ACB=∠ECD=90°,AC=BC=12,DC=EC=5.当点A.C、D在同一条直线上时,AF的长度为_______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们规定:若关于x的一元一次方程ax=b的解为b+a,则称该方程为“和解方程”. 例如:方程2x=﹣4的解为x=﹣2,而﹣2=﹣4+2,则方程2x=﹣4为“和解方程”.
请根据上述规定解答下列问题:
(1)已知关于x的一元一次方程3x=m是“和解方程”,求m的值;
(2)已知关于x的一元一次方程﹣2x=mn+n是“和解方程”,并且它的解是x=n,求m,n的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:数轴上点A表示的数是8,点B表示的数是﹣4.动点P从点A出发,以每秒6个单位长度的速度沿数轴向左运动,动点Q从点B出发,以每秒4个单位长度的速度沿数轴向左运动.P,Q两点同时出发.
![]()
(1)经过多长时间,点P位于点Q左侧2个单位长度?
(2)在点P运动的过程中,若点M是AP的中点,点N是BP的中点,求线段MN的长度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠ACB=90°,AC=BC,AE为BC边上的中线,过点C作CF⊥AE,垂足为点F,在直线CF上截取CD=AE.
(1)求证:BD⊥BC;
(2)若AC=12 cm,求BD的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com