
【题目】如图,在△ABC中,∠ACB=90°,AC=BC,AE为BC边上的中线,过点C作CF⊥AE,垂足为点F,在直线CF上截取CD=AE.
(1)求证:BD⊥BC;
(2)若AC=12 cm,求BD的长.
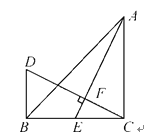
【答案】(1)证明见解析;(2) BD=6 cm.
【解析】
(1)由∠ACB=90°,CF⊥AE于点F易证∠EAC=∠BCD,这样结合AC=BC,AE=CD即可证得△AEC≌△CDB,从而可得∠DBC=∠ACE=90°,由此即可得到BD⊥BC;
(2)由AC=BC,AC=12cm可得BC=12cm,结合AE是△ABC的中线可得CE=6cm,这样由(1)中所得△AEC≌△CDB即可得到BD=CE=6cm.
(1)∵在△ABC中,∠ACB=90°,
∴∠EAC+∠AEC=90°,
∵CF⊥AE,
∴∠BCD+∠AEC=90°,∴∠EAC=∠BCD.
在△AEC和△CDB中, ,
,
∴△AEC≌△CDB(SAS),
∴∠DBC=∠ACE=90°,
∴BD⊥BC;
(2)∵AC=BC,AC=12cm,
∴BC=12cm,
∵AE是BC边上的中线,
∴CE=![]() BC=6cm,
BC=6cm,
∵△AEC≌△CDB,
∴BD=CE=6 cm.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】如图①是一个直角三角形纸片,∠A=30°,将其折叠,使点C落在斜边上的点C处,折痕为BD,如图②,再将②沿DE折叠,使点A落在DC′的延长线上的点A′处,如图③,若折痕DE的长是![]() cm,则BC的长是( )
cm,则BC的长是( )
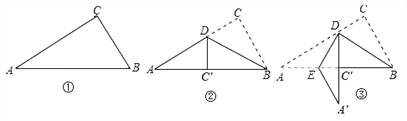
A. 3cm B. 4cm C. 5cm D. 6cm
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知四边形ABCD中,AD∥BC,∠C=90°,P是CD上一点,BH⊥AP于H,BH=BC=CD
(1)求证:∠ABP=45°;
(2)若BC=20,PC=12,求AP的长.
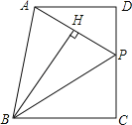
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知点O到△ABC的两边AB,AC所在直线的距离相等,且OB=OC.
(1)如图①,若点O在边BC上,求证:AB=AC;
(2)如图②,若点O在△ABC的内部,求证:AB=AC;
(3)若点O在△ABC的外部,AB=AC成立吗?请画图表示.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了了解某市初中学生上学的交通方式,从中随机调查了a名学生的上学交通方式,统计结果如图. 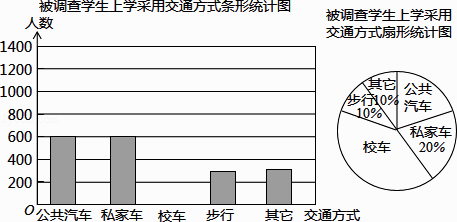
(1)求a的值;
(2)补全条形统计图并求出乘坐公共汽车上学占上学交通方式百分比的扇形圆心角的度数;
(3)该市共有初中学生15000名,请估计其中坐校车上学的人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列结论:w
①若a+b+c=0,且abc≠0,则方程a+bx+c=0的解是x=1;
②若a(x﹣1)=b(x﹣1)有唯一的解,则a≠b;
③若b=2a,则关于x的方程ax+b=0(a≠0)的解为x=﹣![]() ;
;
④若a+b+c=1,且a≠0,则x=1一定是方程ax+b+c=1的解;
其中结论正确个数有( )
A.4个 B.3个 C.2个 D.1个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图, 已知点A、点B是直线上的两点,AB =12厘米,点C在线段AB上,且AC=8厘米.点P、点Q是直线上的两个动点,点P的速度为1厘米/秒,点Q的速度为2厘米/秒.点P、Q分别从点C、点B同时出发,在直线上运动,则经过 秒时线段PQ的长为5厘米.
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
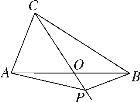
【题目】(题文)如图,在△ABC中,AB=BC=4,AO=BO,P是射线CO上的一个动点,∠AOC=60°,则当△PAB为直角三角形时,AP的长为________________(提示:直角三角形斜边上的中线等于斜边的一半).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,某计算装置有一數据输入口A和一运算结果的输出口B,表格中是小明输入的一些数据和这些数据经该装置计算后输出的相应结果,按照这个计算装置的计算规律,若输入的数是10,则输出的数是( )
A | 1 | 2 | 3 | 4 | 5 |
B | 0 | 3 | 8 | 15 | 24 |
A. 99 B. 100 C. 101 D. 102
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com