
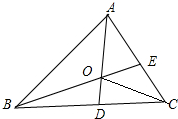
 如图,AD和BE是△ABC的角平分线且交于点O,连接OC,现有以下论断:
如图,AD和BE是△ABC的角平分线且交于点O,连接OC,现有以下论断:| A. | 2 | B. | 3 | C. | 4 | D. | 5 |
分析 根据角平分线的定义判断出OC是∠ACB的平分线,判断出①正确;根据角平分线的定义表示出∠OAC+∠OCA,再根据三角形的内角和定理列式整理即可得到∠AOC=90°+$\frac{1}{2}$∠ABC,判断出②正确;再判断出③④错误,根据三角形的内角和定理和三角形的一个外角等于与它不相邻的两个内角的和求出∠AOE+∠DCO=90°,判断出⑤正确.
解答 解:∵AD和BE是△ABC的角平分线且交于点O,
∴点O是△ABC的角平分线的交点,
∴OC平分∠ACB,故①正确;
由角平分线的定义,∠OAC+∠OCA=$\frac{1}{2}$(∠BAC+∠BCA)=$\frac{1}{2}$(180°-∠ABC)=90°-$\frac{1}{2}$∠ABC,
在△OAC中,∠AOC=180°-(90°-$\frac{1}{2}$∠ABC)=90°+$\frac{1}{2}$∠ABC,故②正确;
只有AB=AC时,OD⊥BC,故③错误;
△ABC是等边三角形时,OA=OB=OC,故④错误;
由三角形的外角性质得,∠AOE=∠OAB+∠OBA=$\frac{1}{2}$(∠BAC+∠ABC),
∠AOE+∠DCO=$\frac{1}{2}$(∠BAC+∠ABC)+$\frac{1}{2}$∠ACB=90°,故⑤正确;
综上所述,正确的结论有①②⑤共3个.
故选B.
点评 本题考查了角平分线上的点到角的两边距离相等的性质,三角形的角平分线的定义,三角形的一个外角等于与它不相邻的两个内角的和的性质,熟记各性质是解题的关键.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
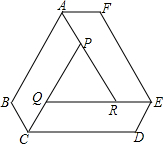 如图,工人师傅要做一张由3块完全相同的平行四边形木板和1块三角板木板拼成的六边形桌面ABCDEF,量得AB=90cm,BC=30cm
如图,工人师傅要做一张由3块完全相同的平行四边形木板和1块三角板木板拼成的六边形桌面ABCDEF,量得AB=90cm,BC=30cm查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com