
分析 (1)观察上面解题过程,得出原式的结果即可;
(2)归纳总结得到一般性规律,写出即可;
(3)原式利用各种分母有理化,计算即可得到结果.
解答 解:(1)原式=$\frac{3(\sqrt{10}+\sqrt{7})}{(\sqrt{10}-\sqrt{7})(\sqrt{10}+\sqrt{7})}$=$\sqrt{10}$+$\sqrt{7}$;
(2)归纳总结得:$\frac{1}{\sqrt{n}+\sqrt{n-1}}$=$\sqrt{n}$-$\sqrt{n-1}$(n≥1);
(3)原式=$\sqrt{2}$-1+$\sqrt{3}$-$\sqrt{2}$+$\sqrt{4}$-$\sqrt{3}$+…+$\sqrt{99}$-$\sqrt{98}$+$\sqrt{100}$-$\sqrt{99}$=10-1=9.
点评 此题考查了分母有理化,弄清题中分母有理化法则是解本题的关键.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{1}{π}$不是单项式 | |
| B. | 多项式-3a2b+7a2b2-2ab+1的次数是3 | |
| C. | 4ab与4xy是同类项 | |
| D. | 2x2-y3是三次二项式 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
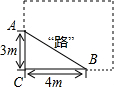 如图,某学校有一块长方形花圃,有极少数人为了避开拐角走“捷径”,在花圃内走出了一条“路”AB,爱心小组想在A处树立一个标牌“少走■米,踏之何刃?”请你计算后帮她们在标牌的■填上适当的数字为2米.
如图,某学校有一块长方形花圃,有极少数人为了避开拐角走“捷径”,在花圃内走出了一条“路”AB,爱心小组想在A处树立一个标牌“少走■米,踏之何刃?”请你计算后帮她们在标牌的■填上适当的数字为2米.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
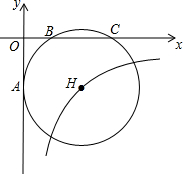 如图所示,经过B(2,0)、C(6,0)两点的⊙H与y轴的负半轴相切于点A,双曲线y=$\frac{k}{x}$经过圆心H,则反比例函数的解析式为-8$\sqrt{3}$.
如图所示,经过B(2,0)、C(6,0)两点的⊙H与y轴的负半轴相切于点A,双曲线y=$\frac{k}{x}$经过圆心H,则反比例函数的解析式为-8$\sqrt{3}$.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
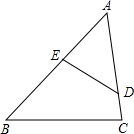 如图,下列条件不能判定△ABC与△ADE相似的是( )
如图,下列条件不能判定△ABC与△ADE相似的是( )| A. | $\frac{AE}{AC}$=$\frac{DE}{BC}$ | B. | ∠B=∠ADE | C. | $\frac{AE}{AD}$=$\frac{AC}{AB}$ | D. | ∠C=∠AED |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 日期 | 1日 | 2日 | 3日 | 4日 | 5日 | 6日 | 7日 |
| 人数变化 | 1.6 | 0.8 | 0.4 | -0.4 | -0.8 | 0.2 | -1.2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com