
| 日期 | 1日 | 2日 | 3日 | 4日 | 5日 | 6日 | 7日 |
| 人数变化 | 1.6 | 0.8 | 0.4 | -0.4 | -0.8 | 0.2 | -1.2 |
分析 (1)根据题目中的数据可以求得每天的人数,从而可以解答本题;
(2)根据9月30日游客人数为5万人和表格中的数据可以求得这7天游客总人数.
解答 解:(1)由题意可得,
10月1日:1.6万人,
10月2日:1.6+0.8=2.4(万人),
10月3日:2.4+0.4=2.8(万人),
10月4日:2.8+(-0.4)=2.4(万人),
10月5日:2.4+(-0.8)=1.6(万人),
10月6日:1.6+0.2=1.8(万人),
10月7日:1.8+(-1.2)=0.6(万人),
∴七天内游客最多的是10月3日,最少的是10月7日;
(2)由题意可得,
这7天游客总人数是:5×7+(1.6+2.4+2.8+2.4+1.6+1.8+0.6)=48.2(万人),
即这7天游客总人数是48.2万人.
点评 本题考查正数和负数,解答本题的关键是明确正数和负数在题目中的实际意义.


 全能测控期末小状元系列答案
全能测控期末小状元系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
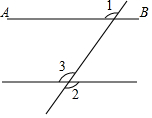 已知,如图,∠1=120°,∠2=120°,求证:AB∥CD.
已知,如图,∠1=120°,∠2=120°,求证:AB∥CD.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com