
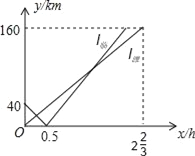
ЁОЬтФПЁП2015Фъ5дТжабЎЃЌжаЙњКЭЖэТоЫЙКЃОќдкЕижаКЃКЃгђОйааСЫДњКХЮЊЁАКЃЩЯСЊКЯЉ2015ЃЈ1ЃЉЁБЕФСЊКЯОќЪТбнЯАЃЌетЪЧжаЙњЕквЛДЮЕижаКЃОйааОќЪТбнЯАЃЌвВЪЧетИіКЃОќОрБОЭСзюдЖЕФвЛДЮОќбнЃЌФГЬьЃЌЁАСйвЪНЂЁБЁЂЁАЮЋЗЛНЂЁБСННЂЭЌЪБДгAЁЂBСНИіИлПкГіЗЂЃЌОљбижБЯпдШЫйЪЛЯђбнЯАФПБъЕиКЃЕКCЃЌСННЂЭЇЖМЕНДяCЕККѓбнЯАЕквЛНзЖЮНсЪјЃЌвбжЊBИеЮЛгкAИлЁЂCИлжЎМфЃЌЧвAЁЂBЁЂCдквЛЬѕжБЯпЩЯЃЌШчЭМЫљЪОЃЌlСйЁЂlЮЋЗжБ№БэЪОЁАСйвЪНЂЁБЁЂЁАЮЋЗЛНЂЁБРыBИлЕФОрРыааЪЛЪБМфx(h)БфЛЏЕФЭМЯѓЃЎ
(1)AИлгыCЕКжЎМфЕФОрРыЮЊ_____ЃЛ
(2)ЗжБ№ЧѓГіЁАСйвЪНЂЁБЁЂЁАЮЋЗЛНЂЁБЕФКНЫйМДЯргіЪБааЪЛЕФЪБМфЃЛ
(3)ШєЁАСйвЪНЂЁБЁЂЁАЮЋЗЛНЂЁБжЎМфЕФОрРыВЛГЌЙ§2kmЪБОЭЪєгкзюМбЭЈбЖОрРыЃЌЧѓГіСННЂЭЇдкбнЯАЕквЛНзЖЮДІгкзюМбЭЈбЖОрРыЪБЕФxЕФШЁжЕЗЖЮЇЃЎ
ЁОД№АИЁПЃЈ1ЃЉ200kmЃЛЃЈ2ЃЉЯргіЪБааЪЛЕФЪБМфЮЊ2hЃЛЃЈ3ЃЉ![]() ЁмxЁм
ЁмxЁм![]() ЃЎ
ЃЎ
ЁОНтЮіЁП
ЃЈ1ЃЉДгЭМЯѓПЩвдПДГіAИлгыCЕКжЎМфЕФОрРыЮЊAЁЂBМфЕФОрРы+BЁЂCМфЕФОрРыОЭПЩвдЧѓГіНсТлЃЛ
ЃЈ2ЃЉИљОнAЁЂBжЎМфЕФОрРыКЭааЪЛЪБМфПЩвдЧѓГіЦфЫйЖШЃЌОЭПЩвдЧѓГіДгBЕНCЕФЪБМфЃЌДгЖјЧѓГіaЃЌИљОнЭМЯѓЧѓГі![]() ЕФНтЮіЪНЃЌШЛКѓгЩЦфНтЮіЪНЙЙГЩЗНГЬзщЧѓГіЦфНтОЭПЩвдЕУГіЁАСйвЪНЂЁБЁЂЁАЮЋЗЛНЂЁБЕФКНЫйМДЯргіЪБааЪЛЕФЪБМфЃЛ
ЕФНтЮіЪНЃЌШЛКѓгЩЦфНтЮіЪНЙЙГЩЗНГЬзщЧѓГіЦфНтОЭПЩвдЕУГіЁАСйвЪНЂЁБЁЂЁАЮЋЗЛНЂЁБЕФКНЫйМДЯргіЪБааЪЛЕФЪБМфЃЛ
ЃЈ2ЃЉЗжСНжжЧщПіСаГіЗНГЬЧѓГіЦфНтОЭПЩвдЕУГіД№АИЃЎ
НтЃКЃЈ1ЃЉгЩЭМЯѓЃЌЕУ
AИлгыCЕКжЎМфЕФОрРыЮЊЃК200kmЃЛ
ЙЪД№АИЮЊЃК200kmЃЛ
ЃЈ2ЃЉЁАСйвЪНЂЁБЕФКНЫйЃК40ЁТ0.5=80ЃЈkm/hЃЉЃЌ
ЁАЮЋЗЛНЂЁБЕФКНЫйЃК160ЁТ2![]() =60ЃЈkm/hЃЉЃЌ
=60ЃЈkm/hЃЉЃЌ
ЫљвдЁАСйвЪНЂЁБДгAЕНCЕФЪБМфa=0.5+160ЁТ80=2.5ЃЌ
Щш![]() ЕФНтЮіЪНЮЊy2=
ЕФНтЮіЪНЮЊy2=![]() xЃЌ
xЃЌ![]() ЕФНтЮіЪНЮЊy1=k1x+b1ЃЌгЩЭМЯѓЕУЃЌ
ЕФНтЮіЪНЮЊy1=k1x+b1ЃЌгЩЭМЯѓЕУЃЌ
160=2![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ
НтЕУЃК![]() =60ЃЌ
=60ЃЌ![]() ЃЌ
ЃЌ
Ёрy2=60xЃЌy1=80xЉ40ЃЌ
ЕБy1=y2ЪБЃЌ
60x=80xЉ40ЃЌ
x=2ЃЌ
ЁрЯргіЪБааЪЛЕФЪБМфЮЊ2hЃЛ
ЃЈ3ЃЉЕБy2Љy1=2ЪБЃЌдђ60xЉЃЈ80xЉ40ЃЉ=2ЃЌ
НтЕУx=![]() ЃЌ
ЃЌ
ЕБy1Љy2=2ЪБЃЌдђЃЈ80xЉ40ЃЉЉ60x=2ЃЌ
НтЕУx=![]() ,
,
ЁрДІгкзюМбЭЈбЖОрРыЪБЕФxЕФШЁжЕЗЖЮЇЮЊ![]() x
x![]() .
.
ЙЪД№АИЮЊЃКЃЈ1ЃЉ200kmЃЛЃЈ2ЃЉЯргіЪБааЪЛЕФЪБМфЮЊ2hЃЛЃЈ3ЃЉ![]() x
x![]() ЃЎ
ЃЎ



| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЩНЕиздааГЕдНРДдНЪмжабЇЩњЕФЯВАЎЃЎвЛЭјЕъОгЊЕФвЛИіаЭКХЩНЕиздааГЕЃЌНёФъвЛдТЗнЯњЪлЖюЮЊ30000дЊЃЌЖўдТЗнУПСОГЕЪлМлБШвЛдТЗнУПСОГЕЪлМлНЕМл100дЊЃЌШєЯњЪлЕФЪ§СПгыЩЯвЛдТЯњЪлЕФЪ§СПЯрЭЌЃЌдђЯњЪлЖюЪЧ27000дЊЃЎ
ЃЈ1ЃЉЧѓЖўдТЗнУПСОГЕЪлМлЪЧЖрЩйдЊЃП
ЃЈ2ЃЉЮЊСЫДйЯњЃЌШ§дТЗнУПСОГЕЪлМлБШЖўдТЗнУПСОГЕЪлМлНЕЕЭСЫ10%ЯњЪлЃЌЭјЕъШдПЩЛёРћ35%ЃЌЧѓУПСОЩНЕиздааГЕЕФНјМлЪЧЖрЩйдЊЃП
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
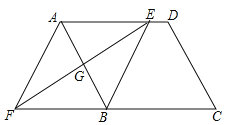
ЁОЬтФПЁПШчЭМЃЌдкЦНааЫФБпаЮABCDжаЃЌБпABЕФДЙжБЦНЗжЯпНЛADгкЕуEЃЌНЛCBЕФбгГЄЯпгкЕуFЃЌСЌНгAFЃЌBEЃЎ
ЃЈ1ЃЉЧѓжЄЃКЁїAGEЁеЁїBGFЃЛ
ЃЈ2ЃЉЪдХаЖЯЫФБпаЮAFBEЕФаЮзДЃЌВЂЫЕУїРэгЩЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПНќЦкЃЌжиЧьЩЬЦЗзЁеЌЪаГЁЗПЮнЯњЪлГіЯжЯњЪлСПКЭЯњЪлМлЦыеЧЬЌЪЦЃЌЪ§ОнЯдЪОЃЌ2016Фъ12дТЃЌМзЁЂввЗПЕиВњЙЋЫОЕФЯњЪлУцЛ§вЛЙВ17000ЦНЗНУзЃЌввЗПЕиВњЙЋЫОЕФЕЅМлЪЧМзЗПЕиВњЙЋЫОЕЅМлЕФ![]() ЃЎМзЗПЕиВњЙЋЫОЕЅМлЮЊУПЦНЗНУз0.8ЭђдЊЃЌСНМвЯњЪлЕФзмН№ЖюЮЊ14430ЭђдЊЃЎ
ЃЎМзЗПЕиВњЙЋЫОЕЅМлЮЊУПЦНЗНУз0.8ЭђдЊЃЌСНМвЯњЪлЕФзмН№ЖюЮЊ14430ЭђдЊЃЎ
ЃЈ1ЃЉЧѓ2016Фъ12дТЃЌМзЁЂввЗПЕиВњЙЋЫОИїЯњЪлСЫЖрЩйЦНЗНУзЃЎ
ЃЈ2ЃЉИљОнЪаГЁашЧѓЃЌМзЁЂввЗПЕиВњЙЋЫООіЖЈЕїећ2017Фъ1дТЗнЕФЗПМлЃЌМзЗПЕиВњЙЋЫОУПЦНЗНУзЕФЪлМлЩЯеЧa%ЃЌЯњЪлСПдЄМЦБШ12дТМѕЩй200ЦНЗНУзЃКввЗПЕиВњЙЋЫООіЖЈвдНЕМлДйЯњЕФЗНЪНгІЖдЕБЧАЕФаЮЪЦЃЌУПЦНЗНУзЕФЪлМлЯТЕї![]() a%ЃЌЯњЪлУцЛ§дЄМЦНЋБШ12дТдіМг700ЦНЗНУзЃЌдЄМЦ1дТЗнСНМвЕФзмЯњЪлЖюЧЁКУЮЊ15310ЭђдЊЃЌЧѓaЕФжЕЃЎ
a%ЃЌЯњЪлУцЛ§дЄМЦНЋБШ12дТдіМг700ЦНЗНУзЃЌдЄМЦ1дТЗнСНМвЕФзмЯњЪлЖюЧЁКУЮЊ15310ЭђдЊЃЌЧѓaЕФжЕЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПМзЁЂввСНШЫНјааТ§ХмСЗЯАЃЌТ§ХмТЗГЬyЃЈУзЃЉгыЫљгУЪБМфtЃЈЗжжгЃЉжЎМфЕФЙиЯЕШчЭМЫљЪОЃЌЯТСаЫЕЗЈДэЮѓЕФЪЧЃЈ ЃЉ

A. ЧА2ЗжжгЃЌввЕФЦНОљЫйЖШБШМзПь
B. 5ЗжжгЪБСНШЫЖМХмСЫ500Уз
C. МзХмЭъ800УзЕФЦНОљЫйЖШЮЊ100Уз/Зж
D. МзввСНШЫ8ЗжжгИїХмСЫ800Уз
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
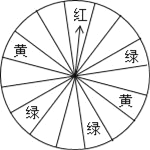
ЁОЬтФПЁПЁАСљвЛЁБЖљЭЏНкЦкМфЃЌФГЩЬЯУЮЊСЫЮќв§ЙЫПЭЃЌЩшСЂСЫвЛИіПЩвдздгЩзЊЖЏЕФзЊХЬЃЈзЊХЬБЛЦНОљЗжГЩ16ЗнЃЉЃЌВЂЙцЖЈЃКЙЫПЭУПЙКТђ100дЊЕФЩЬЦЗЃЌОЭФмЛёЕУвЛДЮзЊЖЏзЊХЬЕФЛњЛсЃЎШчЙћзЊХЬЭЃжЙКѓЃЌжИеые§КУЖдзМФФИіЧјгђЃЌЙЫПЭОЭПЩвдЛёЕУЯргІЕФНБЦЗЃЎ
беЩЋ | НБЦЗ |
КьЩЋ | ЭцОпам |
ЛЦЩЋ | ЭЏЛАЪщ |
ТЬЩЋ | ВЪБЪ |
аЁУїКЭТшТшЙКТђСЫ125дЊЕФЩЬЦЗЃЌЧыФуЗжЮіМЦЫуЃК
(1)аЁУїЛёЕУНБЦЗЕФИХТЪЪЧЖрЩйЃП
(2)аЁУїЛёЕУЭЏЛАЪщЕФИХТЪЪЧЖрЩйЃП
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊЃКABЪЧЁбOЕФжБОЖЃЌжБЯпCPЧаЁбOгкЕуCЃЌЙ§ЕуBзїBDЁЭCPгкDЃЎ 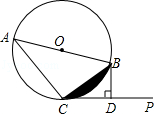
ЃЈ1ЃЉЧѓжЄЃКCB2=ABDBЃЛ
ЃЈ2ЃЉШєЁбOЕФАыОЖЮЊ2ЃЌЁЯBCP=30ЁуЃЌЧѓЭМжавѕгАВПЗжЕФУцЛ§ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПдкжБНЧЁїABCжаЃЌЁЯCЃН90ЁуЃЌDEЁЭACгкEЃЌНЛABгкD.
(1)ЪджИГіBCЁЂDEБЛABЫљНиЪБЃЌЁЯ3ЕФЭЌЮЛНЧЁЂФкДэНЧКЭЭЌХдФкНЧЃЛ
(2)ЪдЫЕУїЁЯ1ЃНЁЯ2ЃНЁЯ3ЕФРэгЩЃЎ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
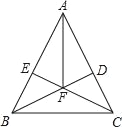
ЁОЬтФПЁПШчЭМЃЌдкЁїABCжаЃЌAB=ACЃЌBDЁЭACгкDЃЌCEЁЭABгкEЃЌBDЁЂCEЯрНЛгкFЃЎ
ЧѓжЄЃКAFЦНЗжЁЯBACЃЎ
ЁОД№АИЁПжЄУїМћНтЮі.
ЁОНтЮіЁПЪдЬтЗжЮіЃКЯШИљОнAB=ACЃЌПЩЕУЁЯABC=ЁЯACBЃЌдйгЩДЙжБЃЌПЩЕУ90ЁуЕФНЧЃЌдкЁїBCEКЭЁїBCDжаЃЌРћгУФкНЧКЭЮЊ180ЁуЃЌПЩЗжБ№ЧѓЁЯBCEКЭЁЯDBCЃЌРћгУЕШСПМѕЕШСПВюЯрЕШЃЌПЩЕУFB=FCЃЌдйвзжЄЁїABFЁеЁїACFЃЌДгЖјжЄГіAFЦНЗжЁЯBACЃЎ
ЪдЬтНтЮіЃКжЄУїЃКЁпAB=AC(вбжЊ)ЃЌ
ЁрЁЯABC=ЁЯACB(ЕШБпЖдЕШНЧ).
ЁпBDЁЂCEЗжБ№ЪЧИпЃЌ
ЁрBDЁЭAC,CEЁЭAB(ИпЕФЖЈвх).
ЁрЁЯCEB=ЁЯBDC=90Ёу.
ЁрЁЯECB=90ЁуЁЯABC,ЁЯDBC=90ЁуЁЯACB.
ЁрЁЯECB=ЁЯDBC(ЕШСПДњЛЛ).
ЁрFB=FC(ЕШНЧЖдЕШБп)ЃЌ
дкЁїABFКЭЁїACFжаЃЌ
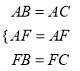 ЃЌ
ЃЌ
ЁрЁїABFЁеЁїACF(SSS)ЃЌ
ЁрЁЯBAF=ЁЯCAF(ШЋЕШШ§НЧаЮЖдгІНЧЯрЕШ)ЃЌ
ЁрAFЦНЗжЁЯBAC.
ЁОЬтаЭЁПНтД№Ьт
ЁОНсЪјЁП
23
ЁОЬтФПЁПШчЭМЃЌдкЁїABCжаЃЌAC=BCЃЌЁЯC=90ЁуЃЌADЪЧЁїABCЕФНЧЦНЗжЯпЃЌDEЁЭABЃЌДЙзуЮЊEЃЎ
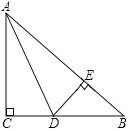
ЃЈ1ЃЉЧѓжЄЃКCD=BEЃЛ
ЃЈ2ЃЉвбжЊCD=2ЃЌЧѓACЕФГЄЃЛ
ЃЈ3ЃЉЧѓжЄЃКAB=AC+CDЃЎ
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com