
����Ŀ��Ϊ������̼�����ɫ���У�ij���г����ֲ�������ĩ��֯��Զ�����С�������г��ӴӼس�����;���ҵض�����Ϣ��ɲ�������������Ŀ�ĵر��أ����г��ӳ���1Сʱ��ǡ��һ���������Ӽس����������г����н�·��ǰ�����أ��ڱ������2Сʱװж������ԭ·���ؼأ����г�������������ʻ�ٶȾ����ֲ��䣬������������ʻ�ٶ������г�����ʻ�ٶȵ�2.5������ͼ��ʾ���г��ӡ���������ص�·��y��km�������г����뿪��ʱ��x��h���ĺ�����ϵͼ�������ͼ���ṩ����Ϣ������и��⣺ 
��1�����г�����ʻ���ٶ���km/h��
��2����������������Сʱ�����г����״�������
��3���������ڷ���;�������г����ٴ�����ʱ�ĵص����ض�Զ��
���𰸡�
��1��24
��2���⣺�������
���������ٶ�Ϊ��24��2.5=60km/h��
������������aСʱ�����������������
24��a+1��=60a��
��ã�a= ![]() ��
��
������������ ![]() Сʱ�����г����״�����
Сʱ�����г����״�����
��3���⣺�����⣬��
������������ص�ʱ��Ϊ��135��60= ![]() ��
��
���������ӱ��س�����ʱ��Ϊ�� ![]() ��
��
��B�� ![]() ��135����C��7.5��0����
��135����C��7.5��0����
���г��ӵ�����ص�ʱ��Ϊ��135��24+0.5= ![]() +0.5=
+0.5= ![]() ��
��
��D�� ![]() ��135����
��135����
��BC�Ľ���ʽΪy1=k1x+b1���������
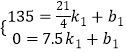 ��
��
�� ![]() ��
��
��y1=��60x+450��
��ED�Ľ���ʽΪy2=k2x+b2���������
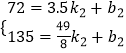 ��
��
��ã� ![]() ��
��
��y2=24x��12��
��y1=y2ʱ��
��60x+450=24x��12��
��ã�x=5.5��
y1=��60��5.5+450=120��
���������ڷ���;�������г����ٴ�����ʱ�ĵص�����120km��
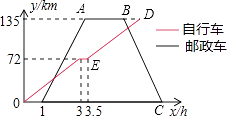
���������⣺��1������������г�����ʻ���ٶ��ǣ�72��3=24km/h�����Դ��ǣ�24����1�����ٶ�=·�̡�ʱ��Ϳ���������ۣ���2�������г����ٶȾͿ���������������ٶȣ�����������������������aСʱ���������������������⼴�ɣ���3�������������ٶȿ������B�������C�����꣬�����г����ٶȾͿ���D�����꣬�ɴ���ϵ�����Ϳ������BC��ED�Ľ���ʽ�Ϳ���������ۣ�



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ѧ����綯����ѧ����ͨ��ȫ����������Ϊ�˽�ij��ѧ2 500��ѧ���ҳ��ԡ���ѧ����綯����ѧ����̬�ȣ������������400���ҳ��������360���ҳ��ַ���̬�ȣ�������˵����ȷ����( )
A. ���鷽ʽ���ղ� B. ��Уֻ��360���ҳ��ַ���̬��
C. ������360���ҳ� D. ��УԼ��90%�ļҳ��ַ���̬��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���������������ij���������ʦ�ڿ����ϳ���һ�������⣺15![]() ��(��8)����һ���������ͬѧ����˴𰸣���ʦ�Ѱ���ͬѧ�Ľ�����̹���д���ڰ��ϣ�
��(��8)����һ���������ͬѧ����˴𰸣���ʦ�Ѱ���ͬѧ�Ľ�����̹���д���ڰ��ϣ�
����һ��ԭʽ��![]() ��(��
��(��![]() )����
)����![]() ����1
����1![]() ��
��
��������ԭʽ��(15��![]() )��(��
)��(��![]() )��15��(��
)��15��(��![]() )��
)��![]() ��(��
��(��![]() )����
)����![]() ����1
����1![]() ��
��
��������ԭʽ��(16��![]() )��(��8)��16��(��8)��
)��(��8)��16��(��8)��![]() ��(��8)����2��
��(��8)����2��![]() ����1
����1![]() .
.
�������ַ�����������۷ף�����Ϊ���ַ�����ã���˵�����ɣ���˵˵��������к�������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������ABCD�У�AB=4��BC=5��AFƽ�֡�DAE��EF��AE����CF=______��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������5�£���ȫ�����ξ��������ȼ�������ϴ���ϲѶ�����С���Բ躣֮�ġ�������ˮ����ҡ������ʻ��й����Ļ��ǡ���������������ҡ�4A�������������ˣ�ȫ�С�4A���������Ѵ�13����ij���ι�˾Ϊ���˽����С�4A����������֪����������ضԲ�����������ֳ��ɷã����������13���������ֵĻش���������������ٷ�Ϊ��Ϥ��A���������˽⣨B��������֪����C����֪֮���٣�D���������ͳ�ƣ�������һ������ͳ��ͼ�����������������ͼ����Ϣ������¸��⣺ 
��1���������������������
��2�����������ڡ������˽⡱���������ˣ�
��3����ȫ����ͳ��ͼ��
��4��������֪������ռ����ͳ��ͼ��Բ�Ľ��Ƕ��ٶȣ���֪֮���١�������ռ�����������İٷֱ��Ƕ��٣�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ȱ���ABC�ı߳���2��D��E�ֱ�ΪAB��AC���е㣬��E����EF��DC��BC���ӳ����ڵ�F������CD��
��1����֤���ı���CDEF��ƽ���ı��Σ�
��2����EF�ij���

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������ABC�У���BAC=90����AD�����ߣ�E��AD���е㣬����A��AF��BC��BE���ӳ�����F������CF�����ж��ı���ADCF����״����֤����Ľ��ۣ�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����һ�ž���ֽƬABCD��ֱ��MN�۵���ʹ��C���ڵ�A������D���ڵ�E����ֱ��MN��BC�ڵ�M����AD�ڵ�N�� 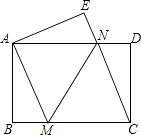
��1����֤��CM=CN��
��2������CMN��������CDN�������Ϊ3��1���� ![]() ��ֵ��
��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����ͼ������һ����ֵת�������������
��1������1���������Ϊ2�����1���������Ϊ1����ô��2���������Ϊ4������1���������Ϊ12�����5���������Ϊ__________��
��2�����������Ϊ5�����2016����������Ƕ��٣�
��3���Ƿ�����������x��ʹ��3�����������x�������ڣ��������x��ֵ���������ڣ���˵�����ɣ�

�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com