Question

【题目】如图，将一张矩形纸片ABCD沿直线MN折叠，使点C落在点A处，点D落在点E处，直线MN交BC于点M，交AD于点N．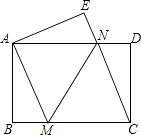
（1）求证：CM=CN；
（2）若△CMN的面积与△CDN的面积比为3：1，求 的值．

Answer 1

【答案】
（1）证明：由折叠的性质可得：∠ENM=∠DNM，

即∠ENM=∠ENA+∠ANM，

∠DNM=∠DNC+∠CNM，

∵∠ENA=∠DNC

∴∠ANM=∠CNM，

∵四边形ABCD是矩形，

∴AD∥BC，

∴∠ANM=∠CMN，

∴∠CMN=∠CNM，

∴CM=CN

（2）解：过点N作NH⊥BC于点H，

则四边形NHCD是矩形，

∴HC=DN，NH=DC，

∵△CMN的面积与△CDN的面积比为3：1，

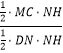∴ = = =3，

∴MC=3ND=3HC，

∴MH=2HC，

设DN=x，则HC=x，MH=2x，

∴CM=3x=CN，

在Rt△CDN中，DC= =2 x，

∴HN=2 x，

在Rt△MNH中，MN= =2 x，

∴ = =2 ．

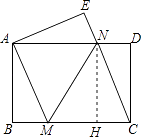
【解析】（1）由折叠的性质可得：∠ANM=∠CNM，由四边形ABCD是矩形，可得∠ANM=∠CMN，则可证得∠CMN=∠CNM，继而可得CM=CN；（2）首先过点N作NH⊥BC于点H，由△CMN的面积与△CDN的面积比为3：1，易得MC=3ND=3HC，然后设DN=x，由勾股定理，可求得MN的长，继而求得答案．