

分析 (1)先根据两角对应相等,判定△ECD∽△BCF,得出$\frac{EC}{BC}$=$\frac{CD}{CF}$,再根据∠FCD=∠BCE,即可得出△ECB∽△DCF,进而得到∠EFD=∠DBE;
(2)先延长BE交AC于点H,判定△HCE∽△HBC,得出HC2=HE•HB,再判定△HAE∽△HBA,得出 HA2=HE•HB,进而得到HC=AH,再根据相似三角形的性质,得出$\frac{DG}{CH}$=$\frac{FG}{AH}$,进而得到DG=FG,再由△DGB∽△CHB得出$\frac{DB}{GF}$=$\frac{CB}{CH}$,最后设AC=2k,则AB=3k,得到BC=$\sqrt{5}$k,CH=$\frac{1}{2}$AC=k,求得$\frac{BC}{CH}$=$\sqrt{5}$,得出$\frac{DB}{GF}$=$\sqrt{5}$,就看得到DB=$\sqrt{5}$GF.
解答 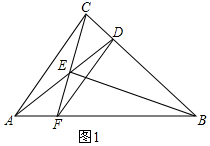 解:(1)如图1,∵∠CED=∠CBA,∠ECD=∠BCF,
解:(1)如图1,∵∠CED=∠CBA,∠ECD=∠BCF,
∴△ECD∽△BCF,
∴$\frac{EC}{BC}$=$\frac{CD}{CF}$,
∵∠FCD=∠BCE,
∴△ECB∽△DCF,
∴∠EFD=∠DBE;
(2)如图2,延长BE交AC于点H,
∵∠CEB=90°,∠HCB=90°,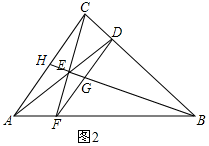
∴∠HCE+∠ECB=∠ECB+∠CBE=90°,
∴∠HCE=∠HBC,
∵∠CHE=∠BHC,
∴△HCE∽△HBC,
∴$\frac{HC}{HB}$=$\frac{HE}{HC}$,
∴HC2=HE•HB,
∵∠EFD=∠DBE=∠ECH,
∴FD∥AC,
∴∠HAE=∠FDE,
∵∠FDE+∠EFD=∠CED,∠FBG+∠EBD=∠CBA,
∴∠FDE=∠EBF,
∴∠HAE=∠EBF,
∵∠EHA=∠AHB,
∴△HAE∽△HBA,
∴$\frac{HA}{HB}$=$\frac{HE}{HA}$,
∴HA2=HE•HB,
∴HC=AH,
∵DF∥HC,
∴△DGB∽△CHB,
∴$\frac{DG}{CH}$=$\frac{GB}{HB}$,
同理可得$\frac{FG}{AH}$=$\frac{GB}{HB}$,
∴$\frac{DG}{CH}$=$\frac{FG}{AH}$,
∴DG=FG,
由△DGB∽△CHB得$\frac{DB}{CB}$=$\frac{DG}{CH}$,即$\frac{DB}{DG}$=$\frac{CB}{CH}$,
∴$\frac{DB}{GF}$=$\frac{CB}{CH}$,
∵∠ACB=90°,cos∠CAB=$\frac{2}{3}$,
设AC=2k,则AB=3k,
∴BC=$\sqrt{5}$k,CH=$\frac{1}{2}$AC=k,
∴$\frac{BC}{CH}$=$\sqrt{5}$,
∴$\frac{DB}{GF}$=$\sqrt{5}$,
∴DB=$\sqrt{5}$GF.
点评 本题属于三角形综合题,主要考查了相似三角形的判定与性质的运用,解决问题的关键是掌握相似三角形的对应边成比例.在判定两个三角形相似时,应注意利用图形中已有的公共角、公共边等隐含条件,以充分发挥基本图形的作用,寻找相似三角形的一般方法是依据基本图形对图形进行分解、组合;或作辅助线构造相似三角形.


 优化作业上海科技文献出版社系列答案
优化作业上海科技文献出版社系列答案科目:初中数学 来源: 题型:解答题
 如图,已知四点A、B、C、D,请用尺规作图完成.(保留画图痕迹)
如图,已知四点A、B、C、D,请用尺规作图完成.(保留画图痕迹)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
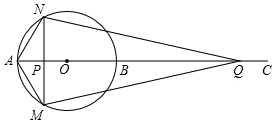 已知:如图,AB为⊙O的直径,点C为AB延长线上一点,动点P从点A出发沿AC方向以1cm/s的速度运动,同时动点Q从点C出发以相同的速度沿CA方向运动,当两点相遇时停止运动,过点P作AB的垂线,分别交⊙O于点M和点N,已知⊙O的半径为2,AC=10,设运动时间为ts.
已知:如图,AB为⊙O的直径,点C为AB延长线上一点,动点P从点A出发沿AC方向以1cm/s的速度运动,同时动点Q从点C出发以相同的速度沿CA方向运动,当两点相遇时停止运动,过点P作AB的垂线,分别交⊙O于点M和点N,已知⊙O的半径为2,AC=10,设运动时间为ts.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,数轴上表示1、$\sqrt{2}$的对应点分别为A、B,点C为点B关于点A的对称点,设点C所表示的数为x.
如图,数轴上表示1、$\sqrt{2}$的对应点分别为A、B,点C为点B关于点A的对称点,设点C所表示的数为x.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com