
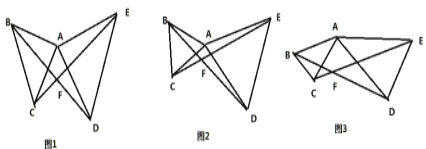
【题目】(1)如图 1,△ABC 和△ADE 都是等腰直角三角形,∠BAC 和∠DAE 是直角,连接BD,CE 相交于点 F,则∠BFC= °
(2)如图 2,△ABC 和△ADE 都是等边三角形,连接 BD,CE 相交于点 F,则∠BFC= °
(3)如图 3,△ABC 和△ADE 都是等腰三角形,AB=AC,AD=AE,且∠BAC=∠DAE,连接 BD,CE相交于点 F,请猜想∠BFC 与∠BAC 有怎样的大小关系?请证明你的猜想
【答案】(1)90°;(2)60°;(3)![]() 证明见解析;
证明见解析;
【解析】
(1)求出![]() 根据SAS证出
根据SAS证出![]() ≌
≌![]() 即可.
即可.
(2)求出![]() 根据SAS证出
根据SAS证出![]() ≌
≌![]() 即可.
即可.
(3)根据![]() 根据SAS证出
根据SAS证出![]() ≌
≌![]() 即可.
即可.
(1)如图:
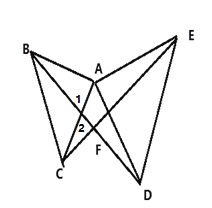
∵△ABC和△ADE都是等腰直角三角形
∴AD=AE,AB=AC,![]()
又∵![]()
∴∠DAB=∠EAC,
∵在△ADB和△AEC中
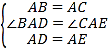 ,
,
∴△ADB≌△AEC(SAS),
∴![]()
∵![]() ,
,![]() ,
,![]()
∴![]()
故答案为:90°
(2)如图:
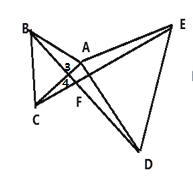
∵△ABC和△ADE都是等边三角形
∴AD=AE,AB=AC,![]()
又∵![]()
∴∠DAB=∠EAC,
∵在△ADB和△AEC中
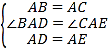 ,
,
∴△ADB≌△AEC(SAS),
∴![]()
∵![]() ,
,![]() ,
,![]()
∴![]()
故答案为:60°
(3) ![]() 理由如下:
理由如下:
∵∠BAC=∠DAE
又∵![]()
∴∠DAB=∠EAC,
∵在△ADB和△AEC中
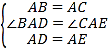 ,
,
∴△ADB≌△AEC(SAS),
∴![]()
∴![]()


科目:初中数学 来源: 题型:
【题目】随着地铁和共享单车的发展,“地铁+单车”已成为很多市民出行的选择,李华从文化宫站出发,先乘坐地铁,准备在离家较近的A,B,C,D,E中的某一站出地铁,再骑共享单车回家,设他出地铁的站点与文化宫距离为x(单位:千米),乘坐地铁的时间y1(单位:分钟)是关于x的一次函数,其关系如下表:
地铁站 | A | B | C | D | E |
x(千米) | 8 | 9 | 10 | 11.5 | 13 |
y1(分钟) | 18 | 20 | 22 | 25 | 28 |
(1)求y1关于x的函数解析式;
(2)李华骑单车的时间(单位:分钟)也受x的影响,其关系可以用y2=![]() x2-11x+78来描述,请问:李华应选择在哪一站出地铁,才能使他从文化宫回到家所需的时间最短?并求出最短时间.
x2-11x+78来描述,请问:李华应选择在哪一站出地铁,才能使他从文化宫回到家所需的时间最短?并求出最短时间.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD的边长为5,点A的坐标为(﹣4,0),点B在y轴上,若反比例函数y=![]() (k≠0)的图象过点C,则该反比例函数的表达式为_______.
(k≠0)的图象过点C,则该反比例函数的表达式为_______.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,Rt△ABO的顶点A是反比例函数y=![]() 与一次函数y=﹣x﹣(k+1)的图象在第二象限的交点,AB⊥x轴于B,且S△ABO=
与一次函数y=﹣x﹣(k+1)的图象在第二象限的交点,AB⊥x轴于B,且S△ABO=![]() .
.
(1)直接写出这两个函数的关系式;
(2)求△AOC的面积;
(3)根据图象直接写出:当x为何值时,反比例函数的值小于一次函数的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“十一”黄金周的某一天,小王全家上午8时自驾小汽车从家里出发,到“番茄农庄”游玩,小汽车离家的距离![]() (千米)与小汽车离家后时间
(千米)与小汽车离家后时间![]() (时)的关系可以用图中的折线表示,根据图像提供的有关信息,解答下列问题:
(时)的关系可以用图中的折线表示,根据图像提供的有关信息,解答下列问题:

(1)“番茄农庄”离家________千米;
(2)小王全家在“番茄农庄”游玩了________小时;
(3)去时小汽车的平均速度是________千米/小时;
(4)回家时小汽车的平均速度是________千米/小时.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知△ABC中,AB=AC, ∠A=40°,O为边BC的中点,把△ABC绕O顺时针旋转m(0<m<180)度后,如果点B恰好落在初始△ABC的边上,那么m=_________
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,∠A的平分线交BC于D,过点D作DE⊥AC,DF⊥AB,垂足为点E、F,下面四个结论中:①∠AEF=∠AFE;②AD垂直平分EF;③S△BFD:S△CED=BF:CE;④EF∥BC,正确的是( )
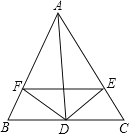
A.①②③B.①③④C.①②④D.②③④
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com